Предмет: Алгебра,
автор: 12344321
Помогите пожалуйста с алгеброй(11 класс). Если не сложно можно полное решение
Приложения:
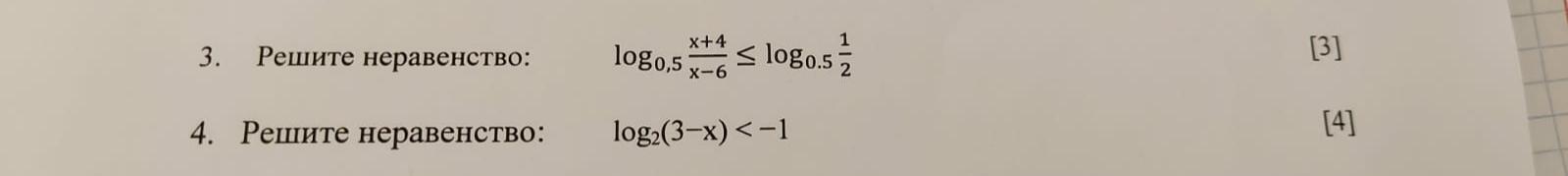
Ответы
Автор ответа:
2
Решение на фотографии
Приложения:

Автор ответа:
2
Решение.
ОДЗ: выражение под знаком log строго больше 0 ,
знаки: +++++(-4) - - - - - (6)+++++
Основание логарифма 0<0,5<1 , поэтому это убывающая функция, и знак между аргументами логарифмической функции будет противоположным .
знаки: +++++ [-14] - - - - (6) +++++
C учётом ОДЗ ответ: .
ОДЗ:
Логарифмическая функция с основанием 2>1 возрастающая, поэтому знак между аргументами логарифмической функции будет таким же .
Учтём ОДЗ:
Ответ: .
Похожие вопросы
Предмет: Русский язык,
автор: наргиза38
Предмет: Русский язык,
автор: bekkalvina2405
Предмет: Окружающий мир,
автор: Соня13223
Предмет: Математика,
автор: vikaniyazova2005
Предмет: Русский язык,
автор: alina0901200432