Предмет: Алгебра,
автор: 12344321
Помогите пожалуйста с алгеброй. Если не сложно можно полное письменное решение(11 класс) заранее благодарю
Приложения:
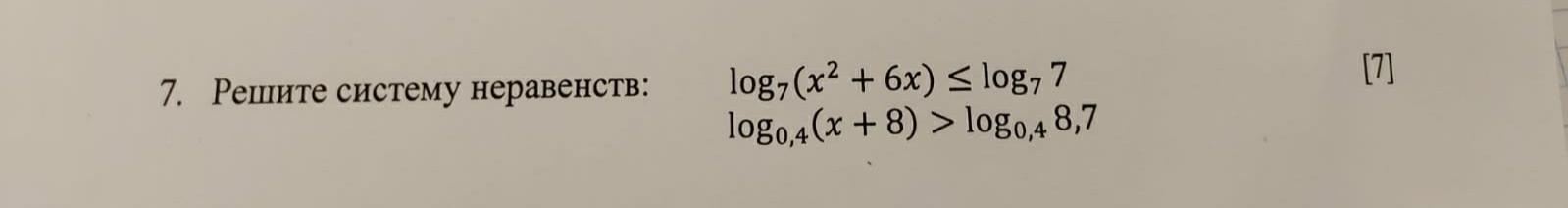
Ответы
Автор ответа:
4
Решение на фотографии.
Приложения:
12344321:
Спасибо большое
Автор ответа:
2
Ответ:
Так как логарифмическая функция с основанием 7>1 возрастающая, а с основанием 0,4<1 - убывающая , то
Решение системы : .
Запишем решение с учётом ОДЗ.
Ответ:
P.S. При решении квадратных неравенств использовали метод интервалов (устно). Записать можно так.
, нули функции :
,
знаки:
.
, корни квадратичной ф-ции по теореме Виета равны
, поэтому
и
,
знаки : .
Спасибо большое
Похожие вопросы
Предмет: Окружающий мир,
автор: Соня13223
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: Viktoria12311
Предмет: Английский язык,
автор: EkatErina0110El
Предмет: Английский язык,
автор: anastasiya2301051