Предмет: Геометрия,
автор: dubkinamaria495
знайти площу поверхні тіла утвореного обертанням рівнобічної трапеції з основами 2 см і 8 см та бічною стороною 5 см навколо більшої основи
zmeura1204:
Якщо ніхто не вирішить, то завтра вирішу.
дякую)
Ответы
Автор ответа:
0
Відповідь:
56π см²
Розв'язання:
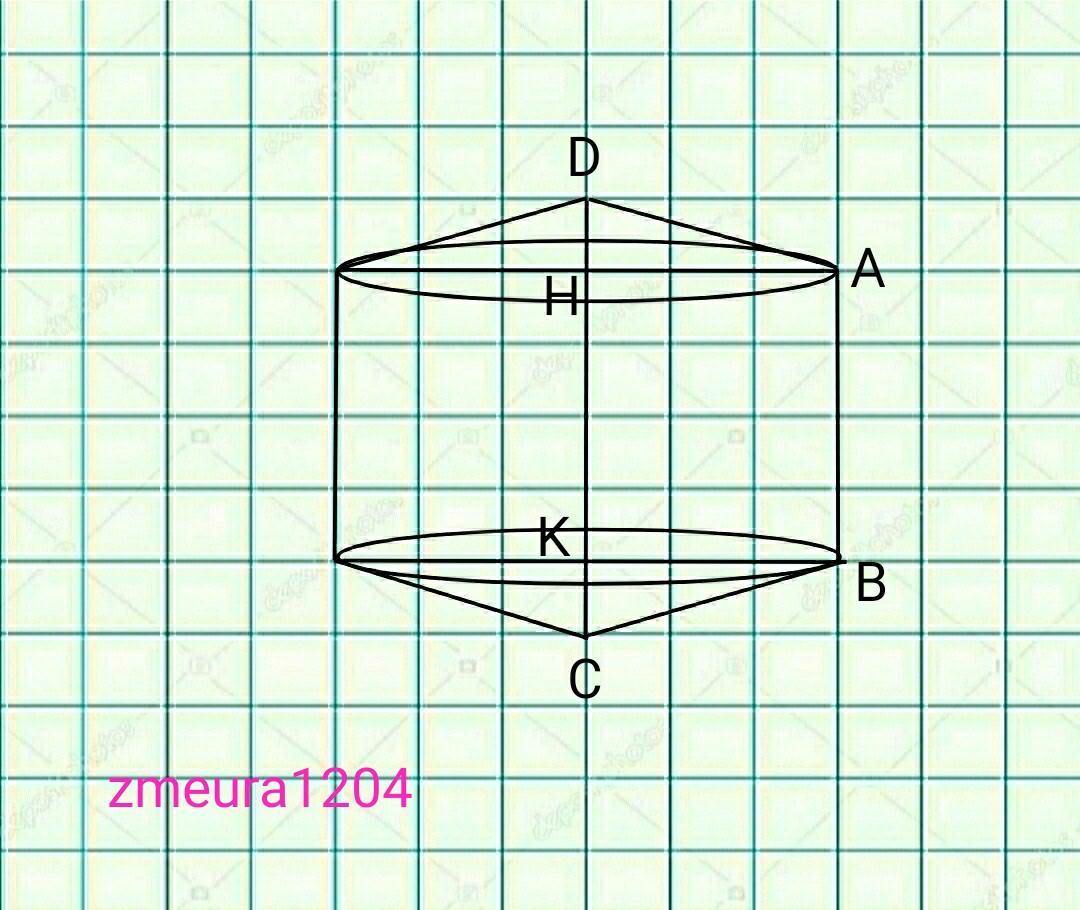
При обертанні трапеції, є два рівні конуса та циліндр.
Sбок.цил.=2πRh;
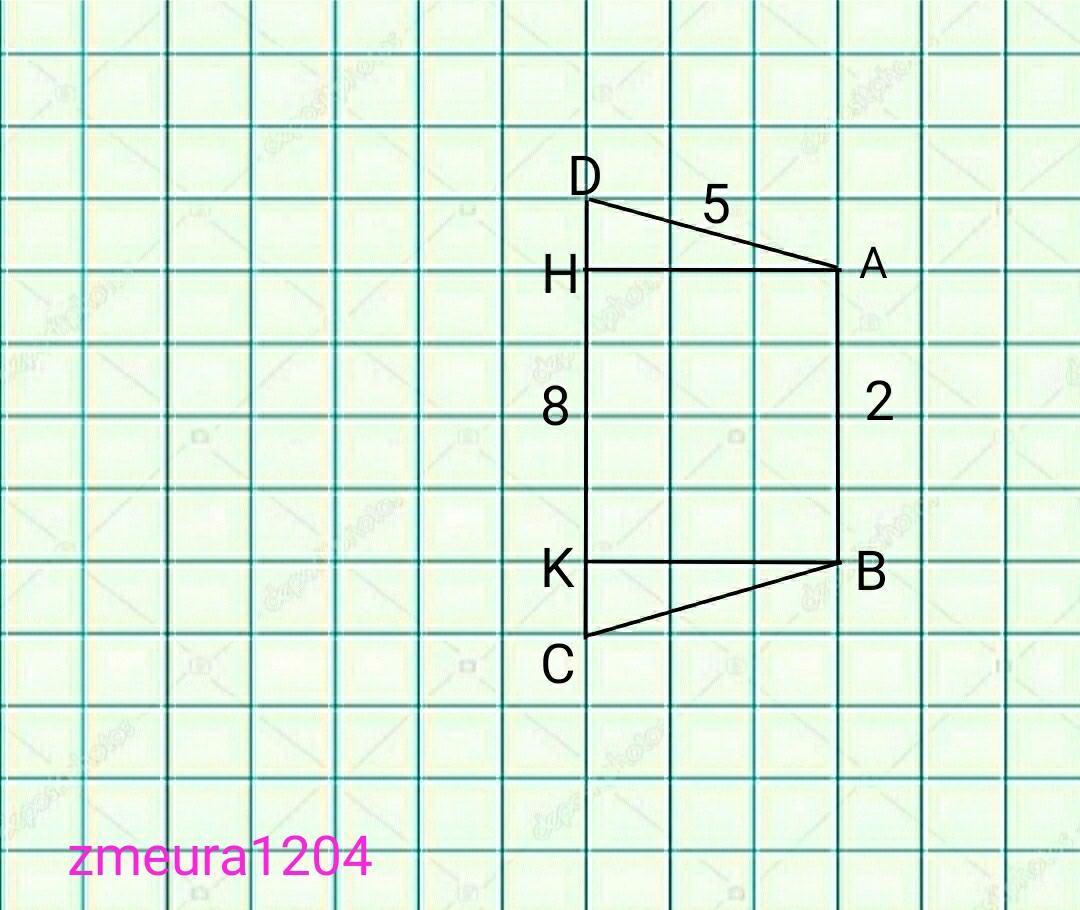
R=KB; h=AB=2см
KC=(DC-AB)/2=(8-2)/2=3см
∆КСВ- прямокутний трикутник.
КВ=√(ВС²-КС²)=√(5²-3²)=4см.
Sбок.цил.=2π*4*2=16π см².
Sбок.кон.=πRL; L=BC=5см; R=4см.
Sбок.кон.=π*4*5=20π см²
Таких конусів два, тож площі також дві.
Sпов.=Sбок.цил.+2*Sбок.кон=
=16π+2*20π=16π+40π=
=56π см²
Позначення:
Sбок.цил.- площа бокової поверхні циліндра.
Sбок.кон.- площа бокової поверхні конуса.
Sпов.- площа повної поверхні.
56π см²
Розв'язання:
При обертанні трапеції, є два рівні конуса та циліндр.
Sбок.цил.=2πRh;
R=KB; h=AB=2см
KC=(DC-AB)/2=(8-2)/2=3см
∆КСВ- прямокутний трикутник.
КВ=√(ВС²-КС²)=√(5²-3²)=4см.
Sбок.цил.=2π*4*2=16π см².
Sбок.кон.=πRL; L=BC=5см; R=4см.
Sбок.кон.=π*4*5=20π см²
Таких конусів два, тож площі також дві.
Sпов.=Sбок.цил.+2*Sбок.кон=
=16π+2*20π=16π+40π=
=56π см²
Позначення:
Sбок.цил.- площа бокової поверхні циліндра.
Sбок.кон.- площа бокової поверхні конуса.
Sпов.- площа повної поверхні.
Приложения:
велике дякую))
Похожие вопросы
Предмет: Русский язык,
автор: юуу1
Предмет: Английский язык,
автор: svetlanavasile2
Предмет: Русский язык,
автор: Samilowaol
Предмет: Литература,
автор: veronika8986