Предмет: Математика,
автор: skeptologskeptolog30
Доказать, что многочлен не имеет кратных корней.
Помогите пожалуйста
Приложения:
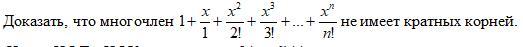
Ответы
Автор ответа:
3
Пусть имеет кратный корень
. Значит, число
является корнем его производной
.
Но тогда является корнем и разности
- но единственным корнем этого многочлена является
. Значит,
.
Но , т.е.
не является корнем
- противоречие.
Значит, не имеет кратных корней.
Ч.т.д.
solka0000:
будь ласка , допоможіть з математикою , я щойно додала завдання , даю максимум балів
Скажите пожалуйста как решать задачи, как вы?(( или это препадают в универах?(
Похожие вопросы
Предмет: Английский язык,
автор: svetlanavasile2
Предмет: Русский язык,
автор: Samilowaol
Предмет: Русский язык,
автор: ннние
Предмет: Физика,
автор: Klirik05
Предмет: Математика,
автор: alia1981