Предмет: Алгебра,
автор: bull62
Мне нужно подробное объяснение задачи . ( написать подробное объяснение задачи )
Вычислить границу функции :

Приложения:
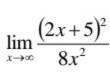
Ответы
Автор ответа:
1
Ответ:
0.5
Объяснение:
По правилу
Получаем следующее :
bull62:
спасибо большое
Похожие вопросы
Предмет: Русский язык,
автор: morozowaga2016
Предмет: Қазақ тiлi,
автор: ДарьяБослер2016
Предмет: Русский язык,
автор: MrGrigo25
Предмет: История,
автор: savenok97
Предмет: Биология,
автор: natashkantl