Предмет: Математика,
автор: anastejsa778
70 БАЛОВ
найти y' по даному уровнение
Приложения:
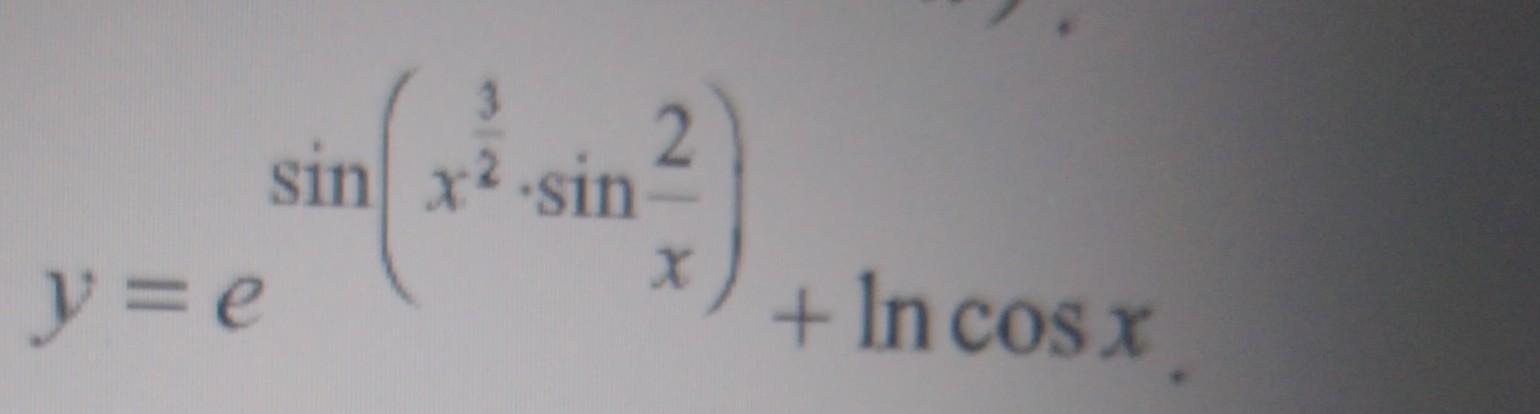
Ответы
Автор ответа:
1
Ответ:
(1/(e^(x²/³sin2/x)+㏑cosx)*((e^(x²/³sin2/x)*cos(x²/³sin2/x)*((3/2)*∛x*sin(2/x)+x³/²*cos(2/x)*-(2/x²))-tgx))
Пошаговое объяснение:
㏑(e^(x²/³sin2/x)+㏑cosx)
y'/y=(1/(e^(x²/³sin2/x)+㏑cosx)*((e^(x²/³sin2/x)*cos(x²/³sin2/x)*((3/2)*∛x*sin(2/x)+x³/²*cos(2/x)*-(2/x²))+(-sinx/cosx))=
(1/(e^(x²/³sin2/x)+㏑cosx)*((e^(x²/³sin2/x)*cos(x²/³sin2/x)*((3/2)*∛x*sin(2/x)+x³/²*cos(2/x)*-(2/x²))-tgx))
anastejsa778:
Спасибо
Похожие вопросы
Предмет: Русский язык,
автор: vadimka1107
Предмет: Русский язык,
автор: ПинкиПай2006
Предмет: Русский язык,
автор: Dahsa3000
Предмет: Математика,
автор: Anastasia200600
Предмет: Математика,
автор: angel06041985