Предмет: Математика,
автор: anastejsa778
100 БАЛОВ Дана функция u=f(x;y). Показать, что она удовлетворяет данному уравнению.
Приложения:
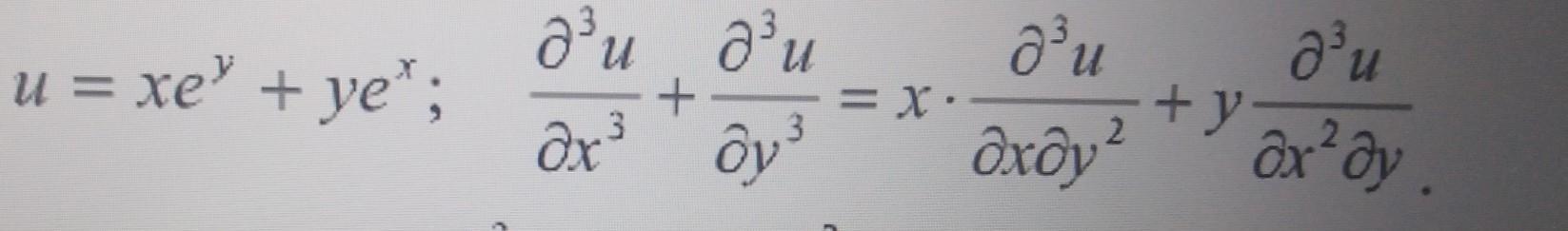
Ответы
Автор ответа:
1
В силу симметрии
Смешанные частные производные одной и той же функции, отличающиеся лишь порядком (очерёдностью) дифференцирования, равны между собой при условии их непрерывности. То есть порядок дифференцирования не важен, можем выбирать какой хотим. Поэтому:
Теперь подставим всё в равенство, которое мы хотим проверить:
, что верно.
anastejsa778:
это просто формулы?
вы про что?
все уже поняла, спасибо за решения
Похожие вопросы
Предмет: Русский язык,
автор: ТугаринЗмей
Предмет: Окружающий мир,
автор: gulya010673
Предмет: Английский язык,
автор: ИльяСамов
Предмет: Алгебра,
автор: sman196747
Предмет: Алгебра,
автор: anvarboy2000