Предмет: Алгебра,
автор: 000000098643
Срочно!!!
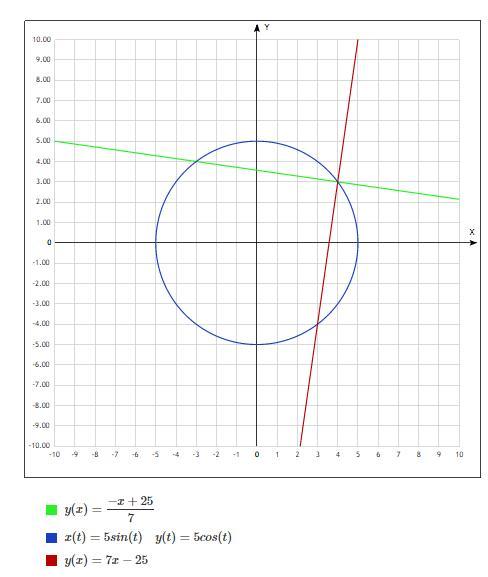
Напишите уравнение прямой, содержащей хорду длины 5√2 окружности, описываемой уравнением x² + y² = 25 и проходящей через точку A = (3,4).
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Так как , координаты точки А(3;4) удовлетворяют уравнение заданной окружности, то точка А - одна из вершин хорды, которую содержит пряммая, проходящая через точку А.
Пусть C(a;b) - другая вершина хорды, тогда имеем систему уравнений (длина АС равна , координаты точки С удовлетворяют уравнение окружности)
(1)
(2)
для C1 (4;-3), A(3;4) AC1: y=kx+b
3=4k+b, 4=-3k+b
4-3=(-3k+b)-(4k+b), 1=-3k+b-4k-b; 1=-7k; k=-1/7;
b=3-4k=3-4*(-1/7)=3+4/7=(21+4)/7=25/7
y=-1/7x+25/7
для C2 (-4;3), A(3;4) AC2: y=kx+b
3=4k+b, -4=3k+b
-4-3=(3k+b)-(4k+b); -7=3k+b-4k-b;-7=-k; k=7
b=3-4k=3-4*7=-25
y=7x-25
Приложения:


Похожие вопросы
Предмет: Русский язык,
автор: дина384
Предмет: Английский язык,
автор: patya8
Предмет: Русский язык,
автор: kunafinatanzilya
Предмет: Математика,
автор: KarinaKristina2008
Предмет: Русский язык,
автор: 787898parol