Предмет: Математика,
автор: dissmaymeow
Изменить порядок интегрирования и вычислить двойной интеграл
Приложения:
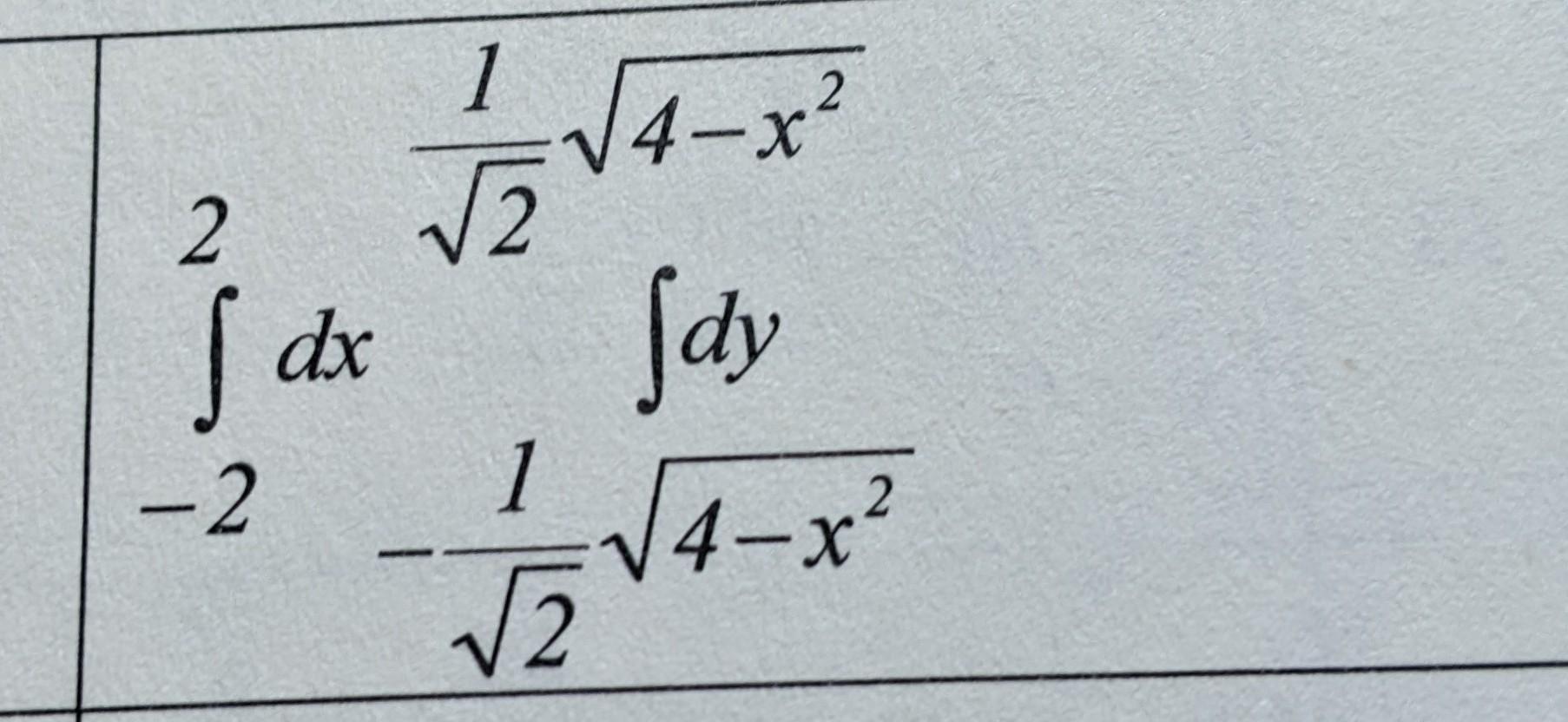
Ответы
Автор ответа:
1
Решение.
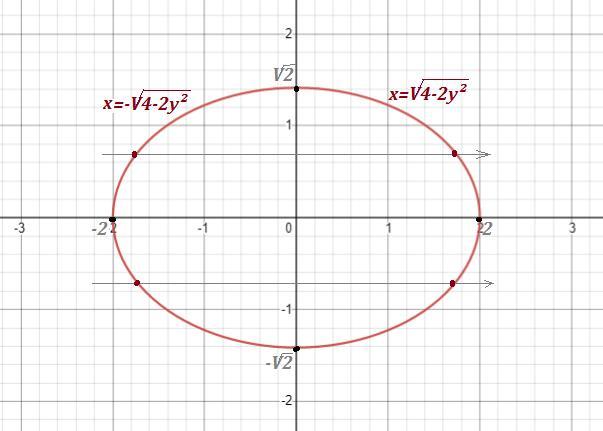
Область, по которой ведётся интегрирование - это эллипс с центром в точке (0,0) , большой полуосью a=2 и малой полуосью b=√2 . Действительно,
- эллипс , центр (0,0) , а=2 , b=√2 .
Выразим переменную х .
Получили уравнения правой и левой половинок эллипса .
Поменяем порядок интегрирования .
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: fersd
Предмет: Английский язык,
автор: Аноним
Предмет: Українська мова,
автор: nastyagurba
Предмет: Литература,
автор: 123118952