Предмет: Алгебра,
автор: DoKDoKDoK
ПОМОГИТЕ! СРОЧНО! РЕШИТЬ СИСТЕМУ УРАВНЕНИЙ МЕТОДОМ ПОДСТАНОВКИ!
Приложения:
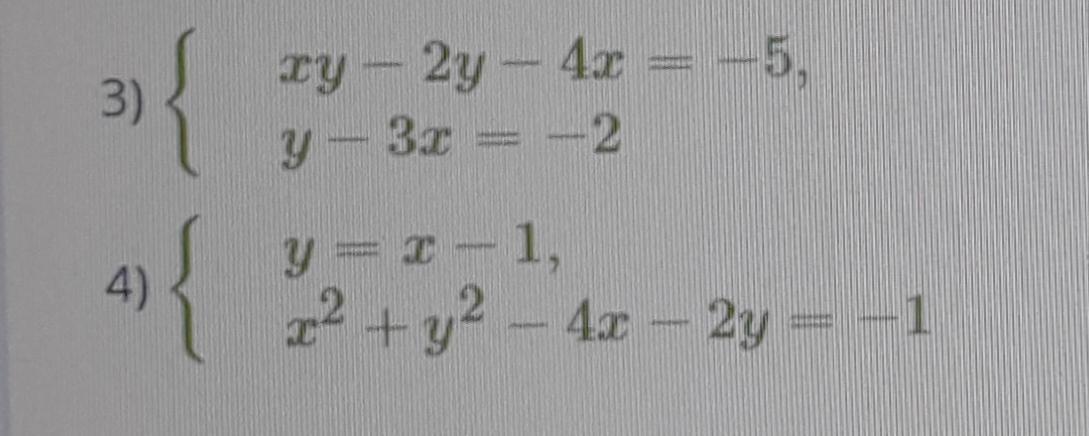
Ответы
Автор ответа:
1
Ответ: (1; 1) и (3; 7)
Ответ:
DoKDoKDoK:
Спас
Автор ответа:
0
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Английский язык,
автор: Cat1905
Предмет: Қазақ тiлi,
автор: Vladinmir
Предмет: История,
автор: Dimas337
Предмет: Математика,
автор: lenaratk