Предмет: Алгебра,
автор: ivanilyshin
Тригонометрические уравнения и неравенства
Приложения:
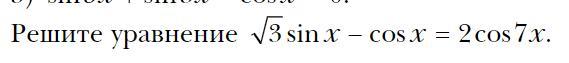
Ответы
Автор ответа:
1
Ответ:
;
, k ∈ Z
Объяснение:
1)
или
2)
k ∈ Z
Похожие вопросы
Предмет: Русский язык,
автор: EmiliNo
Предмет: Русский язык,
автор: lyuba22354564
Предмет: Русский язык,
автор: Рассказик1
Предмет: Геометрия,
автор: nikolayromanovdmitri
Предмет: Русский язык,
автор: Аноним