1,0, 1137. Один из углов треугольника на 15° больше второго и на 9° меньше третьего. Найдите углы этого треугольника. 99 216 помогите пожалуйста
Ответы
Ответ:
62; 47; 71
Пошаговое объяснение:
Сумма углов треугольника 180°
Первый > второго на 15°
первый < третьего на 9°
Пусть первый равен х.
Тогда второй х-15
третий х+9
уравнение
х+(х-15)+(х+9)=180
3х-6=180
3х=180+6
3х=186
х=186/3=62 - это первый
второй х-15=62-15=47°
третий х+9=62+9=71°
Ответ:
Угол А - 62, Угол В - 47, Угол С - 71.
Пошаговое объяснение:
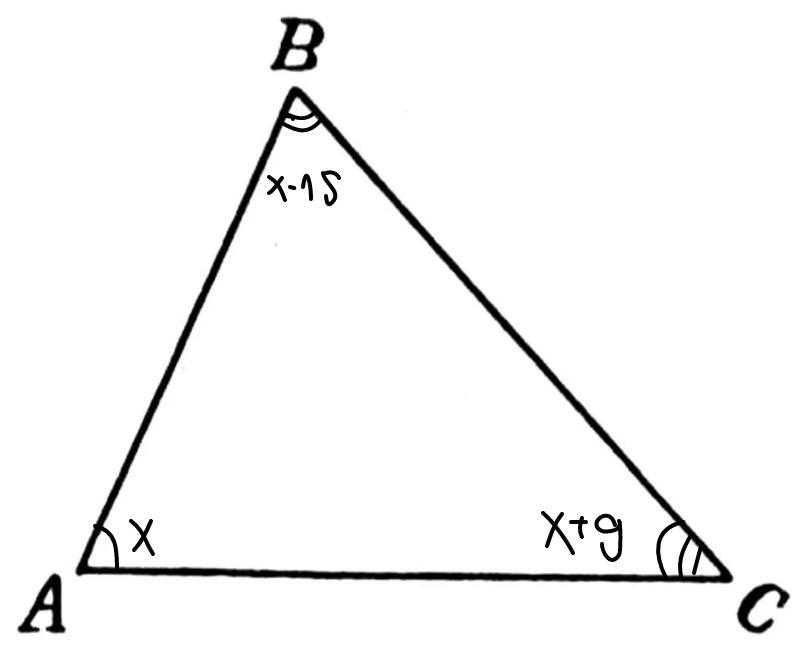
Сначала лучше нарисовать рисунок. Я нарисую треугольник АВС. (см. рисунок)
Легче всего решить уравнением. За Х берём угол А, тогда угол С - х+9, а угол В - х-15
Так как сумма всех углов = 180, составим уравнение:
х + х - 15 + х + 9 = 180
Переносим слагаемые с Х в левую сторону, а без Х (то есть просто числа) - в правую, при этом их знаки меняются:
3х = 180 + 15 - 9
Подсчитываем числа:
3*х = 186
Решаем обычное линейное уравнение:
х = 186 : 3
Находим Х:
х = 62 - угол А, т. к. мы брали угол А за Х.
Теперь легко найти угол В:
62 - 15 = 47 - угол В
Находим угол С:
62 + 9 = 71 - угол С
Ответ:62, 47, 71.
Сделайте пожалуйста ответ лучшим, нажмите на корону внизу!