Предмет: Алгебра,
автор: Pusen
Помогите решить систему!! 25 баллов даю
Приложения:
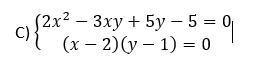
Ответы
Автор ответа:
1
Решение в прикреплённом фото.
Приложения:

Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: olgakolechkina
Предмет: Українська мова,
автор: anerhija
Предмет: Қазақ тiлi,
автор: kulumshin
Предмет: Литература,
автор: alenedaalekssss1234