Предмет: Алгебра,
автор: VladimirAnohov
Задана квадратичная функция y = x2 − 4x + 5
а) Найдите координаты вершины параболы
б) Постройте график данной функции
в) Укажите промежутки возрастания и убывания данной функции
Ответы
Автор ответа:
20
Ответ:
В решении.
Объяснение:
Задана квадратичная функция y = x² − 4x + 5;
а) Найдите координаты вершины параболы;
х₀ = -b/2a;
x₀ = 4/2
x₀ = 2;
y = x² − 4x + 5;
y₀ = 2² - 4 * 2 + 5 = 4 - 8 + 5 = 1;
y₀ = 1;
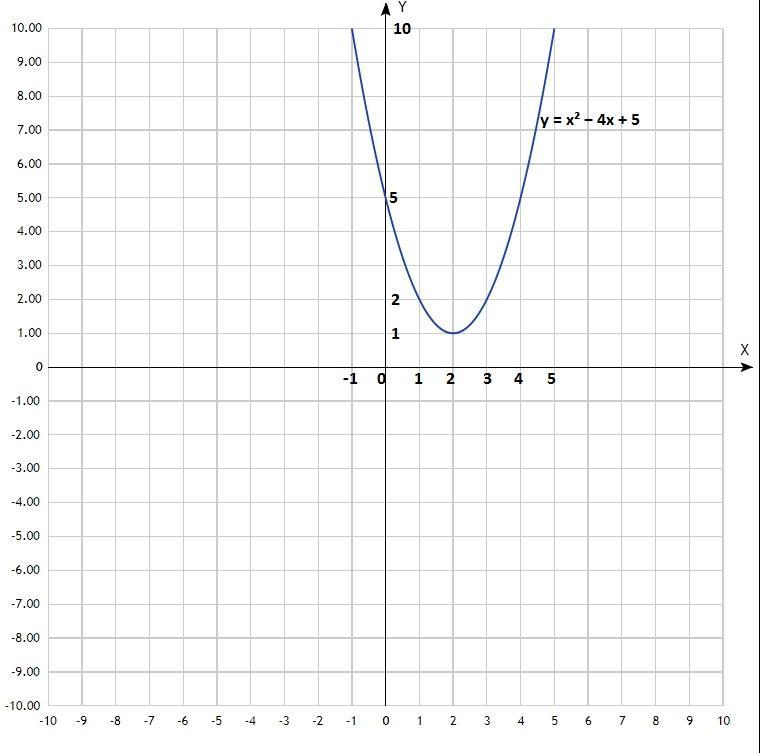
Координаты вершины параболы: (2; 1).
б) Постройте график данной функции;
Уравнение квадратичной функции, график - парабола со смещённым центром, ветви направлены вверх.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
y = x² − 4x + 5;
Таблица:
х -1 0 1 2 3 4 5
у 10 5 2 1 2 5 10
По вычисленным точкам построить параболу.
в) Укажите промежутки возрастания и убывания данной функции;
Функция возрастает при х∈(2; +∞);
Функция убывает при х∈(-∞; 2).
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: катюшаАбрамович
Предмет: Русский язык,
автор: chupsmils03
Предмет: Русский язык,
автор: gogogof123
Предмет: Математика,
автор: miui635
Предмет: Окружающий мир,
автор: nurchikkrut360