Предмет: Математика,
автор: vavvy8577
Помогите решить математике тройной интеграл
Приложения:
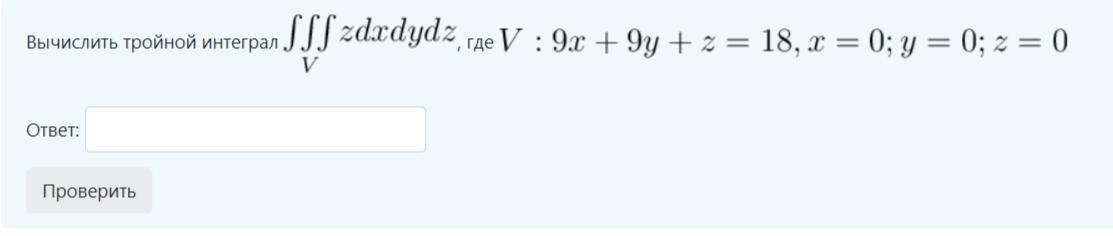
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Область интегрирования - плоскость:
9x + 9y + z = 18
Запишем уравнение плоскости в отрезках:
Интервалы:
x₀ = 0; x₁ = 2
y₀ = 0; y₁ = 2
z₀ = 0; z₁ = 18
Похожие вопросы
Предмет: Английский язык,
автор: GalinaR11
Предмет: Английский язык,
автор: морпврмлб
Предмет: Русский язык,
автор: checkmeout
Предмет: Русский язык,
автор: soy70
Предмет: Математика,
автор: hooligan48