Задание приложено...
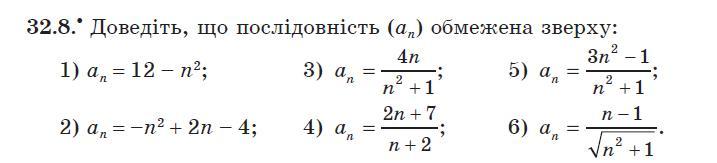
Ответы
Ответ:
По определению:
Числовую последовательность называют ограниченной сверху, если существует такое число
, что для любого
выполняется неравенство
.
(Определение через кванторы: )
То есть необходимо найти такое число , чтобы выполнялось неравенство
и эти доказать, что последовательность ограниченна сверху.
32.8
1)
Проанализируем выражение . От числа 12 отнимается какое-то целое положительное число и с увеличением
это число возрастает. Тогда можно предположить, что число 12 удовлетворяет условию:
, где
. Докажем данное утверждение.
при
, то есть доказано, что последовательность
является ограниченное сверху.
2)
Преобразуем последовательность:
Можно предположить, что максимальный элемент последовательности это первый, то есть
Тогда можно предположить, что число -3 удовлетворяет условию: , где
. Докажем данное утверждение.
при
, то есть доказано, что последовательность
является ограниченное сверху.
3)
Докажем, что последовательность является возрастающей, то есть верно утверждение, что
для
.
- данное неравенство свидетельствует о том, что гипотеза оказалась неверное. Модифицируем гипотезу и докажем, что последовательность является невозрастающей, то есть что
, что с учетом выше сделанных преобразований можно записать в виде неравенства
, что нужно доказать.
Преобразуем полином
То есть доказано, что последовательность является невозрастающей.
Найдем первый элемент последовательности .
.
То есть так как последовательность является невозрастающей,
то можно сделать гипотезу, что что число 2 удовлетворяет условию: , где
. Докажем данное утверждение.
при
, то есть доказано, что последовательность
является ограниченное сверху.
4)
Преобразуем последовательность :
С увеличением числа дроби
и
уменьшаются, так как
стоит в знаменателе, тогда можно предположить, что число
удовлетворяет условию:
, где
. Докажем данное утверждение.
при
, то есть доказано, что последовательность
является ограниченное сверху.
Продолжение решения смотрите на фотографиях!!!

