Задание приложено...
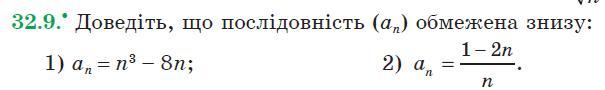
Ответы
Ответ:
По определению:
Числовую последовательность называют ограниченной снизу, если существует такое число
, что для любого выполняется
неравенство
.
(Определение через кванторы: )
То есть необходимо найти такое число , чтобы выполнялось неравенство
и этим доказывается по определению, что последовательность ограниченна снизу.
32.9
1)
Найдем первый элемент последовательности
Можно сделать гипотезу, что что число -7 удовлетворяет условию: , где
. Докажем данное утверждение.
Так как при
, то доказав данное неравенство при
вместо
докажем более сильное утверждение, тогда и при
неравенство также будет выполнятся, то есть необходимо доказать, что
.
Так как число может быть произвольным, то можем взять число -16, так как если при -16 верно, то и при большем
также верно по свойству транзитивности, то есть при -7.
Тогда с учетом всех модификаций необходимо доказать неравенство:
при
и теперь необходимо доказать, что
и
Тогда если , то все предыдущие условие будут выполняться, то есть при
доказано, что последовательность
является ограниченной снизу.
2)
Преобразуем последовательность :
К числу каждый раз добавляется какое-то число
, поэтому можно предположить, что что число -2 удовлетворяет условию:
, где
. Докажем данное утверждение.
То есть при доказано, что последовательность
является ограниченной снизу.