Предмет: Математика,
автор: rkia978
Срочно! Нужно решить...
Приложения:
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
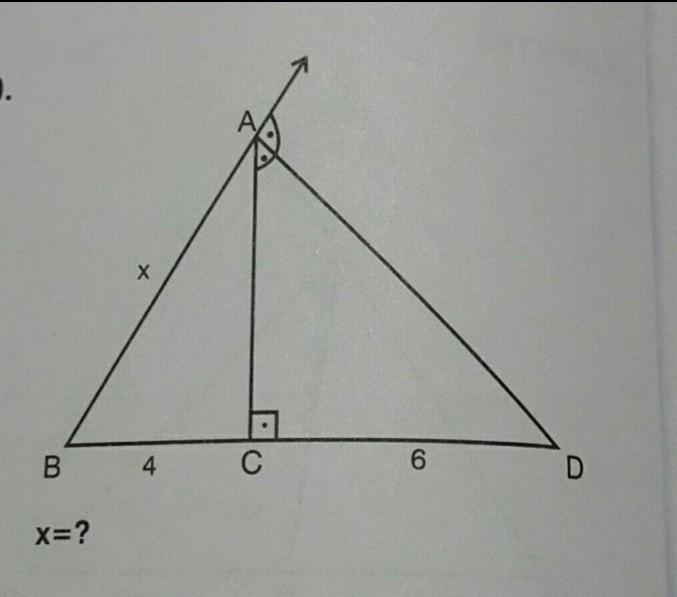
Введём обозначение: AD = y.
Выразим катет AC, пользуясь теоремой Пифагора:
Найдём неизвестную сторону через площади треугольника:
С другой стороны, площадь треугольника можно найти по формуле Герона:
Упростим подкоренное выражение:
rkia978:
Спасибо Огромное!
:)
Пожалуйста.
Похожие вопросы
Предмет: Английский язык,
автор: Тони111111
Предмет: Окружающий мир,
автор: кри8888
Предмет: Русский язык,
автор: 45n1
Предмет: Биология,
автор: ansarkaamiraaa
Предмет: Русский язык,
автор: DUDURICHkristina