Предмет: Алгебра,
автор: antomaria33073307
Даю 35 балів, допоможіть, будь ласка
Приложения:
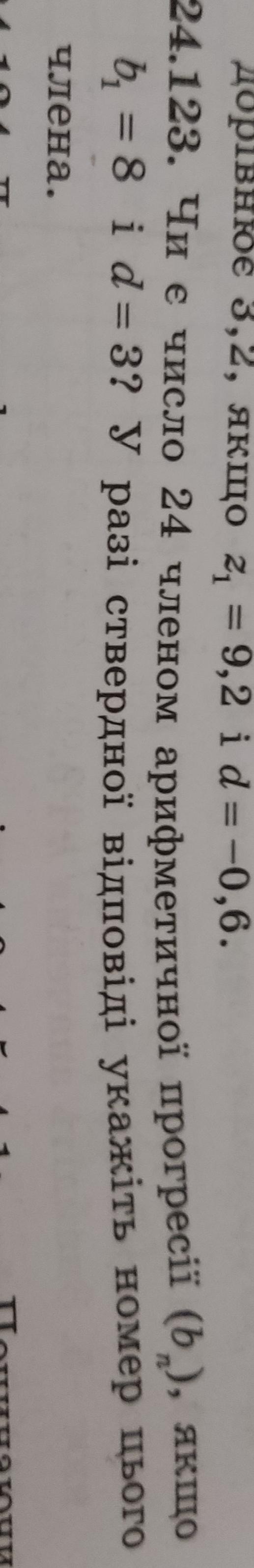
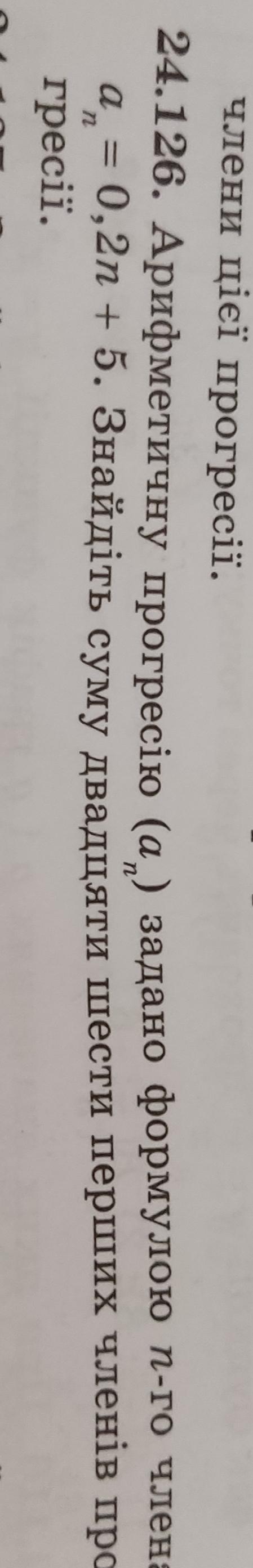
Ответы
Автор ответа:
1
Решение.
24.123. Арифм. прогрессия .
n-ый член арифм. прогрессии . Подставим числа.
Так как получили натуральное число n=8 , то делаем вывод, что число 24 - это член заданной арифм. прогрессии с номером 8 .
24.126. Арифм. прогрессия
Найдём .
.
Похожие вопросы
Предмет: Қазақ тiлi,
автор: 20aishat04
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Dloordd
Предмет: Русский язык,
автор: Kseniya25003