Предмет: Алгебра,
автор: cvcvczxz
НАПИШИТЕ НА ЛИСТИКЕ ПОЖАЛУЙСТА РЕШЕНИЕ
Приложения:
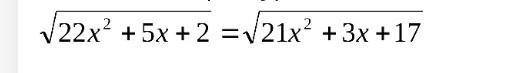
Ответы
Автор ответа:
0
Ответ:
Возведём обе части уравнения , которые принимают неотрицательные значения, в квадрат.
Чтобы не решать громоздкое ОДЗ, сделаем проверку. Подставим числовые значения х в уравнение .
Похожие вопросы
Предмет: Қазақ тiлi,
автор: arina9631
Предмет: Русский язык,
автор: lexalexa2006
Предмет: Русский язык,
автор: vertsanova
Предмет: Русский язык,
автор: Динабат
Предмет: Қазақ тiлi,
автор: akbota9156