Question

СРОЧНО! На рисунке поставить буквы: Δ АВС (АВС = 90°),

Δ МNК (МNК = 90°). Доказать равенство треугольников подробно.
Даю 10 баллов

Answer 1

Ответ:

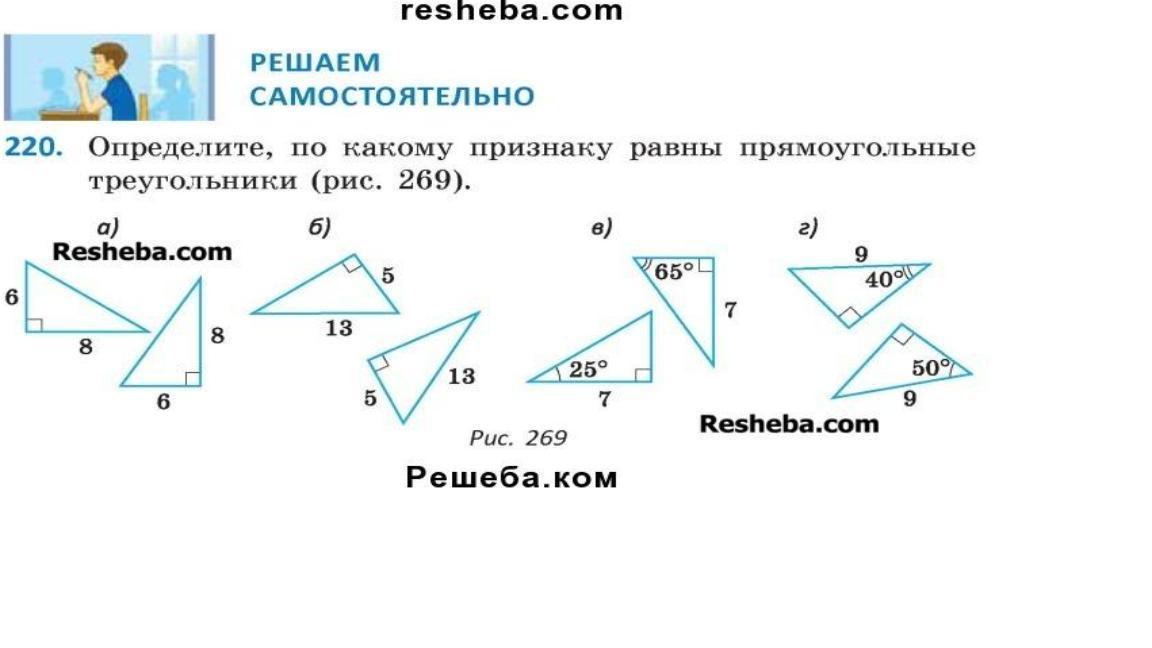
а) по двум катетам

б) по гипотенузе и катету

в) по катету и прилежащему острому углу

г) по гипотенузе и острому углу.

Объяснение:

Признаки равенства прямоугольных треугольников:

( 1 ) по двум катетам

Если катеты одного треугольника соответственно равны катетам другого треугольника, то такие прямоугольные треугольники равны.

( 2 ) по катету и прилежащему острому углу

Если катет и прилежащий острый угол одного треугольника соответственно равны катету и прилежащему острому углу другого треугольника, то такие прямоугольные треугольники равны.

( 3 ) по гипотенузе и острому углу

Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие прямоугольные треугольники равны.

( 4 ) по гипотенузе и катету

Если гипотенуза и катет одного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие прямоугольные треугольники равны.

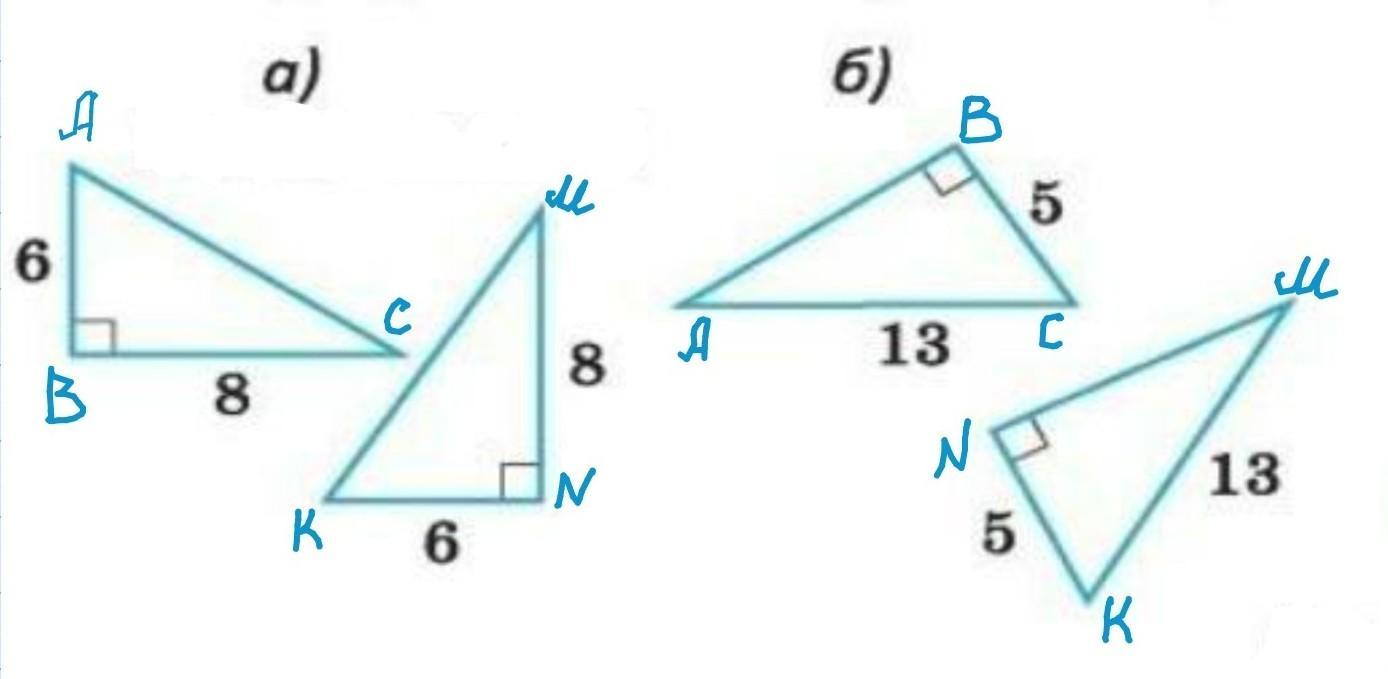
Рассмотрим прямоугольные треугольники △ABC (∠ABC=90°) и△MNK(∠MNK=90°).

а) Так как соответствующие катеты равны: AB=NK=6ед, а BC=MN=8ед, то

△ABC =△KNM по двум катетам.

б) AC=MK=13 ед, BC=NK=5ед. Так как гипотенуза AC равна гипотенузе MK, а катет BC равен катету KN, то △ABC =△MNK по гипотенузе и катету.

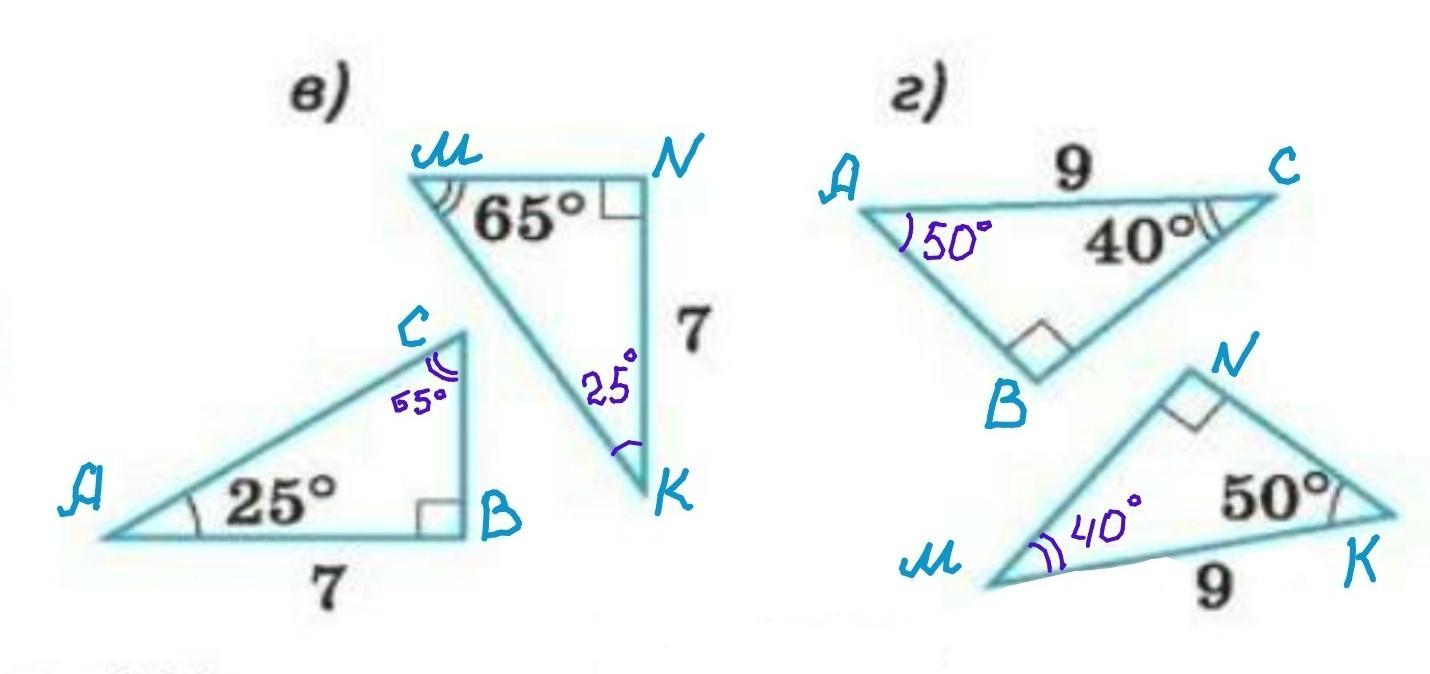
в) Сумма острых углов в прямоугольном треугольнике равна 90°. ∠K=90°-∠M=90°-65°=25°.

Таким образом ∠K=∠A=25°, прилещащие к этим углам катеты также равны: AB=NK=7 ед.

△ABC =△KNM по катету и прилежащему острому углу

г) Гипотенузы равны: AC=MK=9ед.

∠A=90°-∠C=90°-40°=50°. Следовательно ∠A=∠K=50°.

△ABC =△KNM по гипотенузе и острому углу.