Предмет: Алгебра,
автор: sergiyknyazevv
СРОЧНО ДАМ 30 БАЛОВ !!!!!!!!!!!!!!!
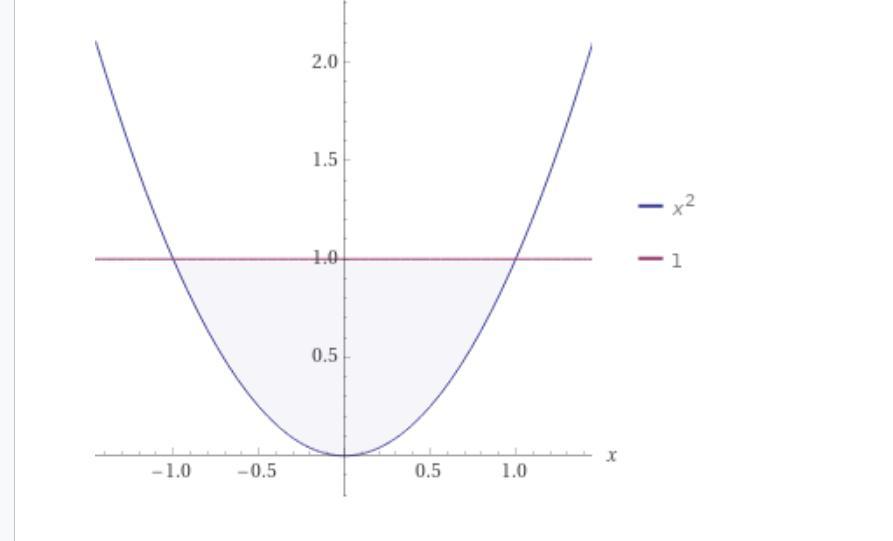
знайти площу фігури обмеженої параболою y=x2 і прямою y=1
Ответы
Автор ответа:
1
Знайти площу фігури обмеженої параболою y=x² і прямою y=1.
Так как прямая у = 1 ограничивает фигуру сверху, то искомая площадь равна интегралу от функции 1 - x².
Осталось найти крайние точки фигуры по оси Ох для вычисления определённого интеграла.
Для этого приравняем значение игрека к 1.
1 = x², отсюда х = +-1.
Тогда S = ʃ-11(1 - x²) = x – (x³/3)| -11 = (1-(1/3)-(-1-(-1/3)) =4/3.
Ответ: S = (4/3) кв. ед.
Приложения:
sergiyknyazevv:
Спасибо!
Похожие вопросы
Предмет: Английский язык,
автор: catmea
Предмет: Другие предметы,
автор: komviragmailcom
Предмет: Русский язык,
автор: Lakilbaeva
Предмет: Алгебра,
автор: kiler95
Предмет: Математика,
автор: verakot13