Предмет: Математика,
автор: SuzukiElen
Помогите решить интеграл, с решением Прошу!!!!
Приложения:
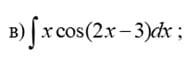
Ответы
Автор ответа:
2
Решение.
Интегрирование по частям .
Похожие вопросы
Предмет: Русский язык,
автор: mskondrateva
Предмет: Английский язык,
автор: Aru12yuss
Предмет: Русский язык,
автор: larachanan201
Предмет: Русский язык,
автор: Аноним