Предмет: Математика,
автор: SuzukiElen
Помогите решить интеграл, с решением Прошу!!!!
Приложения:
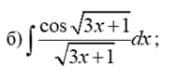
Ответы
Автор ответа:
0
Ответ:
Примечание:
По таблице интегралов:
Пошаговое объяснение:
--------------------------------------------
Замена:
-----------------------------------------------
Похожие вопросы
Предмет: Немецкий язык,
автор: barabahka53
Предмет: Русский язык,
автор: ggur
Предмет: Қазақ тiлi,
автор: aidasaburova
Предмет: География,
автор: tanasis92