Предмет: Математика,
автор: SuzukiElen
Помогите пожалуйста решить интеграл !!! Если можно с решением, прошу !!!
Приложения:
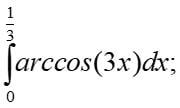
Ответы
Автор ответа:
1
Решение.
Интегрирование по частям.
Похожие вопросы
Предмет: Русский язык,
автор: Ellizabet2017
Предмет: Русский язык,
автор: Poleshuklyubov
Предмет: Русский язык,
автор: lilk67
Предмет: Математика,
автор: dmitripolihko84