Предмет: Математика,
автор: SuzukiElen
Помогите пожалуйста решить интеграл !!!
Приложения:
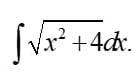
Ответы
Автор ответа:
1
Ответ:
Интегрируем по частям.
Обратим внимание на то, что в правой части получили тот же интеграл, что и был задан , но со знаком минус . То есть интеграл свёлся к самому себе !
Похожие вопросы
Предмет: Українська мова,
автор: Аноним
Предмет: Другие предметы,
автор: школарасии2
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: TinoLlLlkoJHNk
Предмет: Литература,
автор: m1leron