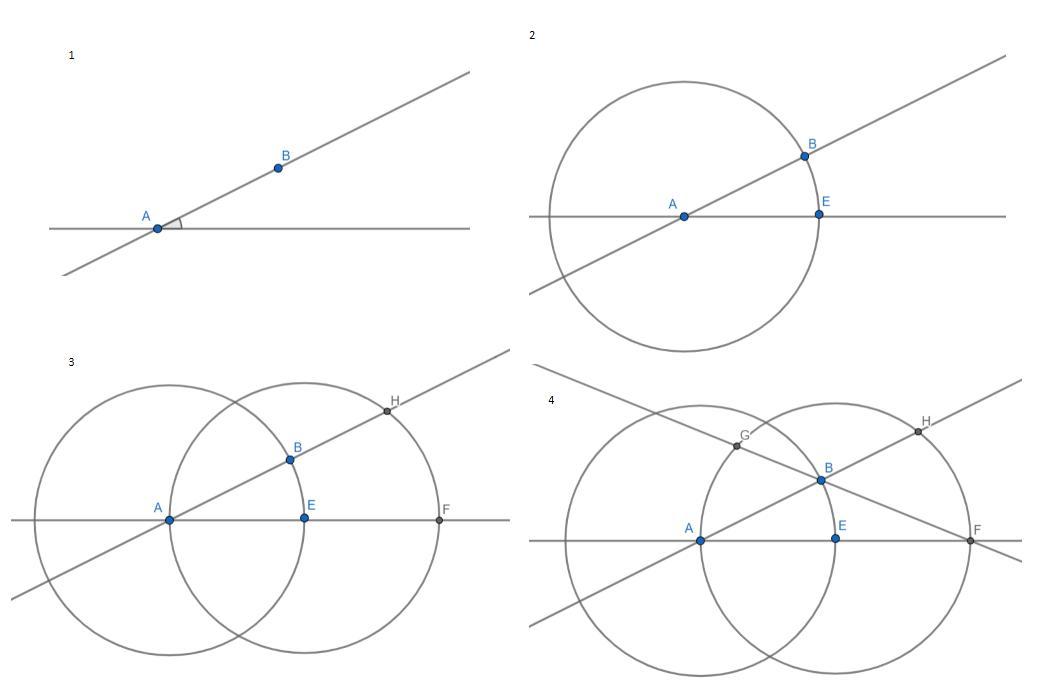
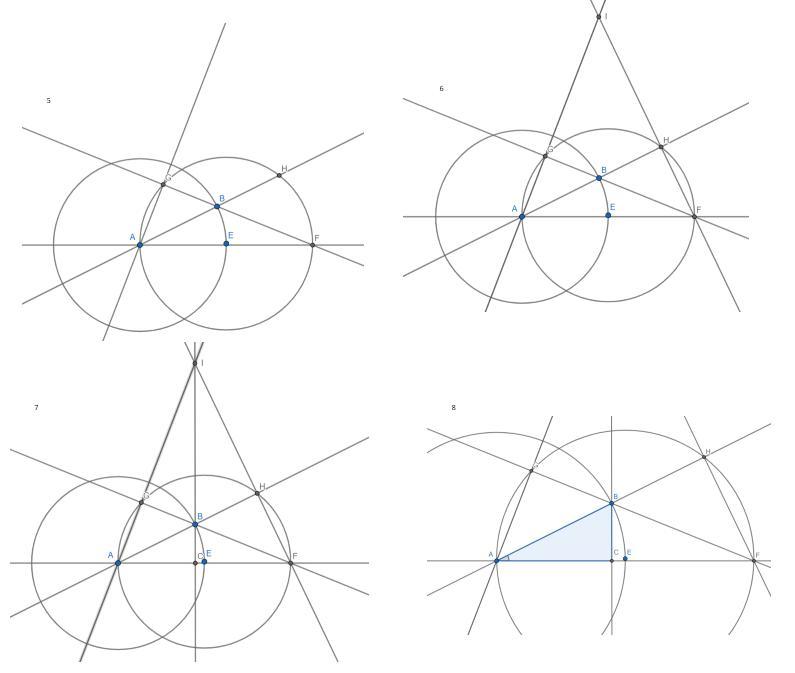
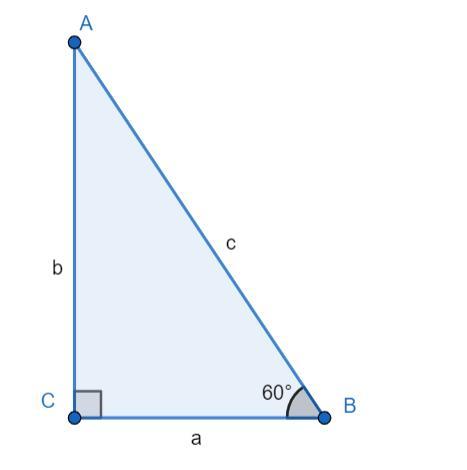
Построить прямоугольный треугольник циркулем и линейкой по гипотенузе и острому углу. 2) Один из углов прямоугольного треугольника равен 60°, сумма меньшего катета и гипотенузы равна 35,7см. Найдите гипотенузу треугольника.
Ответы
Ответ:
1) построение в приложенных рисунках.
2) гипотенуза равна 23,8 см
Объяснение:
1) Построение с помощью циркуля и линейки по этапам представлено на приложенных рисунках. Прокомментирую 7 картинку, почему угол BCA является прямым: в окружности с центром в точке Е и радиусом EA треугольники AGF, AHF являются прямоугольными, как вписанные в окружность треугольники, с одной стороной, являющейся диаметром окружности - соответственно тогда FG и AH являются высотами AIF, и точка B является точкой пересечения высот этого треугольника - значит прямая IB также будет являться высотой в треугольника AIF -значит BC⊥CA
2) Рисунок прикрепил ниже. a+c=35,7см, ∠B=60°. Нужно найти с.
Так как ∠B=60°, то ∠A=30°, и c=2a - подставим это выражение a+c:
a+c=35,7
a+2a=35,7
a=35,7/3=11,9
c=2a=11,9*2=23,8