Question

Докажите что две хорды окружности которые не проходят через её центр пересекаясь не могут делиться пополам.


Помогите пожалуйста. Дам 30 баллов

Answer 1

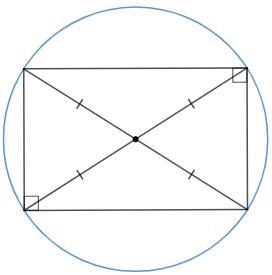
Рассмотрим хорды как диагонали вписанного четырехугольника. Если диагонали четырехугольника точкой пересечения делятся пополам, то четырехугольник - параллелограмм и его противоположные углы равны. Так как четырехугольник вписанный, сумма противоположных углов 180°. Следовательно, эти углы по 90°. Значит, они опираются на диаметр.

Доказали, что вписанный параллелограмм - прямоугольник, диагонали являются диаметрами.

Соответственно, если хорды не проходят через центр, не являются диаметрами, то противоположные углы четырехугольника не прямые, не равные, а значит четырехугольник не параллелограмм и не может иметь признак параллелограмма - его диагонали не могут точкой пересечения делиться пополам.