Предмет: Математика,
автор: studentsezs17
Добрый день, помогите пожалуйста найти определённый интеграл "СРОЧНО".
Приложения:
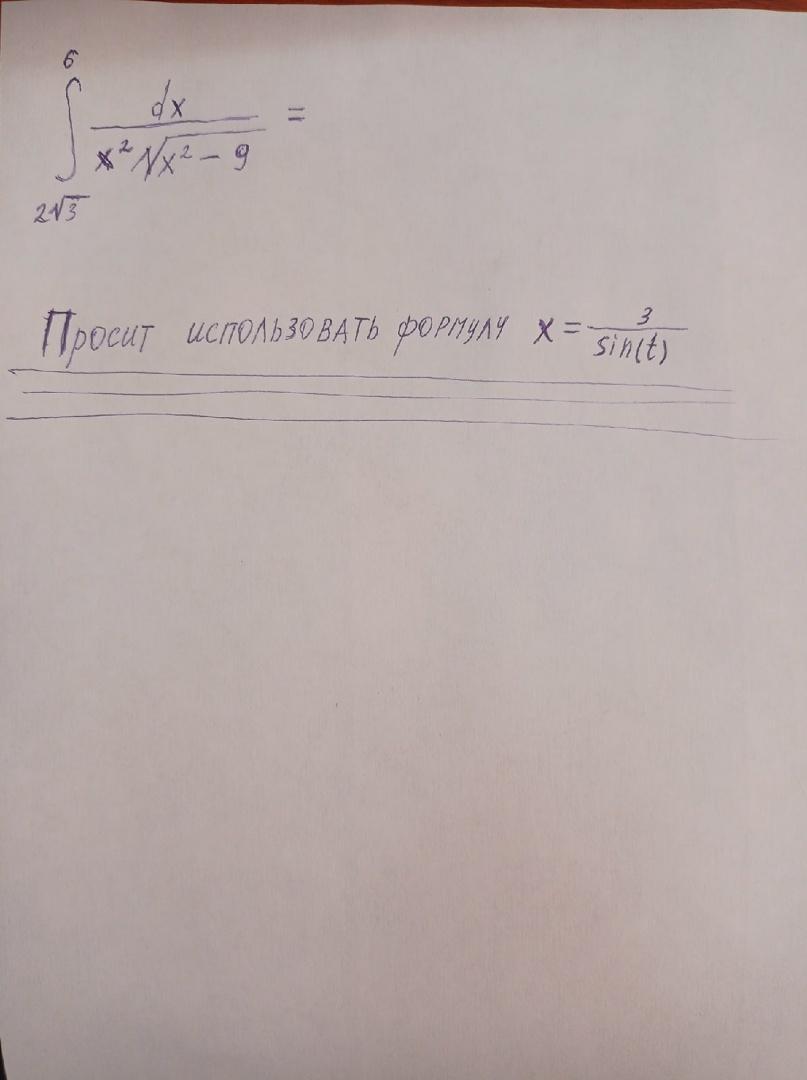
Ответы
Автор ответа:
1
Ответ:
Метод замены переменной .
studentsezs17:
Большое спасибо
Похожие вопросы
Предмет: Русский язык,
автор: ДиляВалитова
Предмет: Русский язык,
автор: Юичиро
Предмет: Французский язык,
автор: александр377
Предмет: Английский язык,
автор: Holdikwin
Предмет: География,
автор: kylinhe9464