Question

основание пирамиды равносторонний треугольник длина стороны 8 см одна боковая грань,которая также является равносторонним треугольником,перпендикулярная основанию две остальные боковые грани образуюс с основанием равные углы.Определи площадь поверхности пирамидыоснование пирамиды равносторонний треугольник длина стороны 8 см одна боковая грань,которая также является равносторонним треугольником,перпендикулярная основанию две остальные боковые грани образуюс с основанием равные углы.Определи площадь поверхности пирамиды

Answer 1

Ответ:

16√3(2+√5) см²

Пошаговое объяснение:

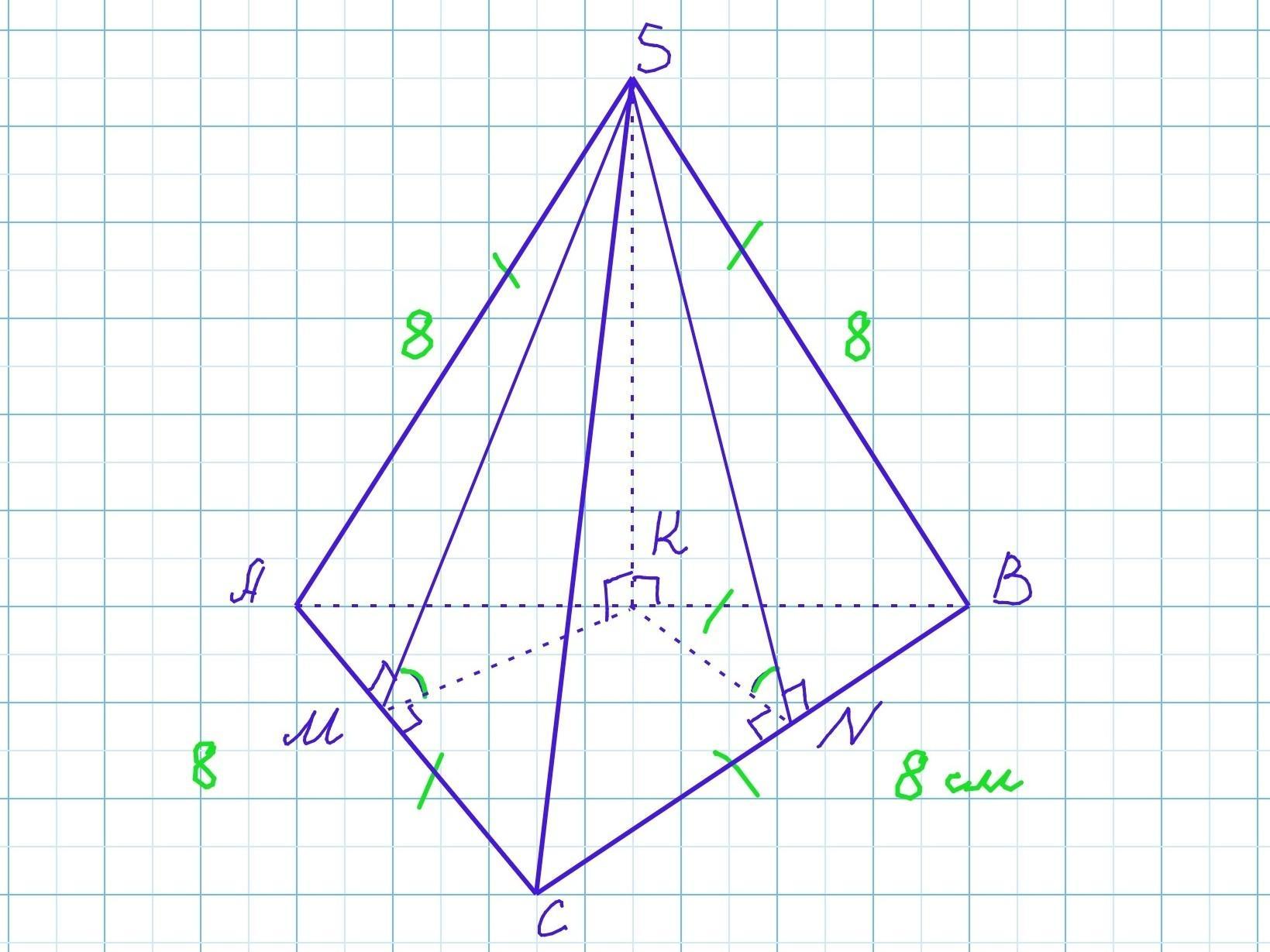
Пусть грань ASB пирамиды SABC перпендикулярна плоскости основания ABC. Так как по условию эта грань является равносторонним треугольником, то высота и медиана SK является также высотой пирамиды. SK⟂AB.

Проведём SM⟂AC и SN⟂BC. По теореме о трёх перпендикулярах KM⟂AC и KN⟂BC. ∠SMK и ∠SNK - линейные углы двугранных углов, образованные боковыми гранями и основанием. По условию они равны.

Рассмотрим прямоугольный треугольник AKM(∠M=90°)

Так как △ABC - равносторонний, то ∠MAK =60°, тогда ∠AKM=30°. AK=4 см (SK - медиана).

AM=2см, как катет лежащий напротив угла в 30°.

Рассмотрим прямоугольный треугольник ASM(∠M=90°)

По теореме Пифагора найдём катет MS:

MS²=AS²-AM²=8²-2²=64-4=60

MS=2√15см

△ABC=△ASB - по условию.

Площадь равностороннего треугольника вычисляется по формуле:

$S = \dfrac{ {a}^{2} \sqrt{3} }{4}$

где а - сторона треугольника.

Тогда:

$S(ABC) = S(ASB) = \dfrac{ {8}^{2} \sqrt{3} }{ 4 } = 16 \sqrt{3}$см²

△ASC=△BSC по трём сторонам (3 признак): AS=SB, AC=BC - как стороны равностороннего треугольника, SC - общая.

Площадь треугольника равна половине произведения основания на высоту.

Тогда:

$S(ASC) = S(BSC) = \frac{1}{2} \times AC \times MS = \frac{1}{2} \times 8 \times 2 \sqrt{15} = 8 \sqrt{15}$см²

Полная площадь поверхности пирамиды:

$S_n = 2 \times (S(ABC) + S(ASC)) = 2 \times (16 \sqrt{3} + 8 \sqrt{15} ) = 16 \sqrt{3} (2 + \sqrt{5)}$см²