Предмет: Математика,
автор: dipseydipsey
50 баллов. найти предел числовой последовательности
Приложения:

Ответы
Автор ответа:
1
Ответ:
Примечание:
Предел частного:
(Детальнее смотрите фотографию)
Пошаговое объяснение:
Приложения:
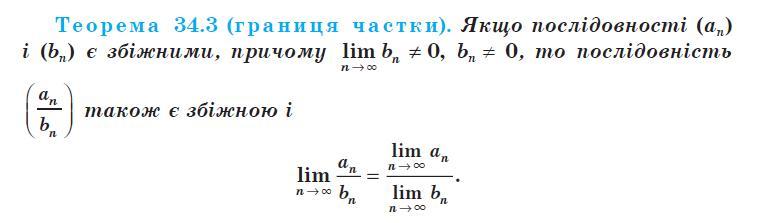
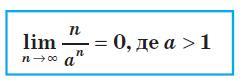
Похожие вопросы
Предмет: Французский язык,
автор: оля1390
Предмет: Русский язык,
автор: аяна1231
Предмет: Русский язык,
автор: maripylka
Предмет: Математика,
автор: kudaibergen57