Question

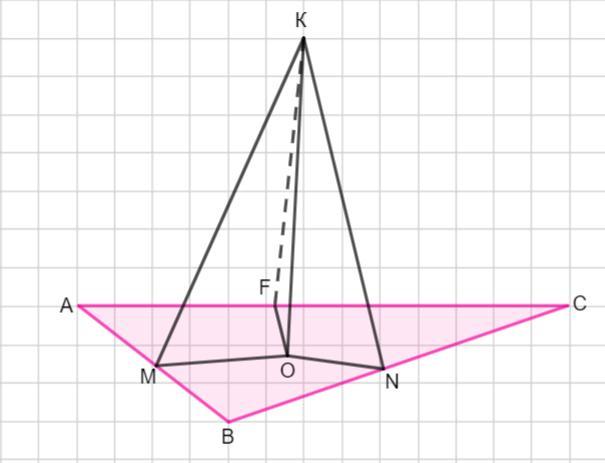
Нехай точка К рівновіддалена від сторін трикутника АВС, довжини сторін якого 15 см, 8 см і 17 см. Знайдіть відстань від цієї точки до сторін трикутника, якщо відстань від точки К до площини трикутника дорівнює 4 см.

Answer 1

Ответ:

Расстояние от точки до стороны треугольника равно 5 см.

Объяснение:

Пусть точка К равноудалена от сторон треугольника АВС, стороны этого треугольника 15 см, 8, см и 17 см. Расстояние от точки К до плоскости треугольника ОК = 4 см.

Если точка К равноудалена от сторон треугольника АВС, то точка О - центр вписанной в тругольник окружности. Это слкдуеи из равенства прямоугольных треугольников .

ΔKOM =ΔKON =Δ KOF по катету и гипотенузе (катет КО общий, а гипотенузы треугольников равны по условию КМ = КN=КF).

Найдем радиус окружности, вписанной в треугольник ΔАВС по формуле

$r=\dfrac{2S}{P}$

$P= 15+8+17 =40$ см.

Данный треугольник прямоугольный, так как

$17^{2} =8^{2} +15^{2} ;\\289=64+225;\\289=289$

По теореме, обратной теореме Пифагора, данный треугольник прямоугольный с катетами 15 см и 8 см.

Найдем площадь треугольника как полупроизведение катетов.

$S= \dfrac{1}{2} \cdot 8\cdot15=4\cdot 15=60$ см².

Тогда радиус, вписанной окружности будет равен

$r=\dfrac{2\cdot 60}{40} =\dfrac{120}{40} =3$ см.

Значит, ОМ =ON= OF =3 см.

Рассмотрим Δ КОМ - прямоугольный. Найдем гипотенузу КМ по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$KM ^{2} =KO^{2} +OM ^{2} ;\\KM=\sqrt{KO^{2} +OM ^{2}} ;\\KM=\sqrt{4^{2}+3^{2} } =\sqrt{16+9} =\sqrt{25} =5$ см.