Question

log(2x-2)2+log(x-1)^2 8 Больше или равно 2

Answer 1

Ответ:

$\left(\dfrac{3}{2};\dfrac{1}{\sqrt[4]{8} } +1\right]$  ∪  $(2;3]$ - решение неравенства .

Объяснение:

Решим неравенство:

$\log{_{(2x-2)}}2 +\log{_{(x-1)^{2} }}8\geq 2$

$\log{_{2(x-1)\)}}2 +\log{_{(x-1)^{2} }}8\geq 2$

Найдем область допустимых значений данного неравенства.

Так как основание логарифма положительное число и не равно единице, то получим систему:

$\left \{\begin{array}{l} 2(x -1) > 0, \\ 2x-2 \neq 1 ,\\(x-1)^{2} > 0, \\ (x-1)^{2} \neq 1 ;\end{array} \right.\Leftrightarrow \left \{\begin{array}{l} x -1 > 0, \\ 2x \neq 3 ,\\x\neq 1, \\x-1\neq -1\\ x-1 \neq 1 ;\end{array} \right.\Leftrightarrow\left \{\begin{array}{l} x > 1, \\ x \neq 1,5 ,\\x\neq 1, \\x\neq 0\\ x \neq 2 ;\end{array} \right.\Leftrightarrow\left \{\begin{array}{l} x > 1, \\ x \neq 1,5 ,\\x\neq 2 \end{array} \right.\Leftrightarrow$

$\Leftrightarrow \left [\begin{array}{l} 1 < x < 1,5 ,\\ 1,5 < x < 2, \\ x > 2.\end{array} \right.$

Воспользуемся формулой перехода к новому основанию и перейдем к основанию 2.

$\dfrac{1}{\log{_2}(2(x-1))} +\dfrac{\log{_2}8}{\log{_2}(x-1)^{2} } -2\geq 0;\\\\\dfrac{1}{\log{_2}2+\log{_2}(x-1)} +\dfrac{3}{2\log{_2}(x-1)} -2\geq 0;\\\\\dfrac{1}{1+\log{_2}(x-1)} +\dfrac{3}{2\log{_2}(x-1)} -2\geq 0;$

Пусть $\log{_2}(x-1)=t$

Тогда неравенство принимает вид:

$\dfrac{1}{1+t} +\dfrac{3}{2t} -2\geq 0;\\\\\dfrac{1}{1+t}^{\backslash2t} +\dfrac{3}{2t} ^{\backslash(t+1}-2^{\backslash2t(t+1)}\geq 0;\\\\\dfrac{2t+3t+3-4t^{2}-4t }{2t(t+1)} \geq 0;\\\\\dfrac{-4t^{2}+t +3}{2t(t+1)} \geq0|\cdot(-1);\\\\\dfrac{4t^{2}-t -3}{2t(t+1)}\leq 0$

Разложим числитель на множители. Для этого решим квадратное уравнение

$4t^{2} -t-3=0;\\D= (-1)^{2} -4\cdot4\cdot(-3)=1+48=49=7^{2} ;\\\\t{_1}=\dfrac{1-7}{2\cdot4} =-\dfrac{6}{8} =-\dfrac{3}{4} ;\\\\t{_2}=\dfrac{1+7}{2\cdot4} =\dfrac{8}{8} =1.$

Тогда

$4t^{2} -t-3=4(t-1)\left(t+\dfrac{3}{4} \right)=(t-1)(4t+3)$

Тогда неравенство принимает вид

$\dfrac{(4t+3)(t-1) }{2t(t+1)}\leq 0$

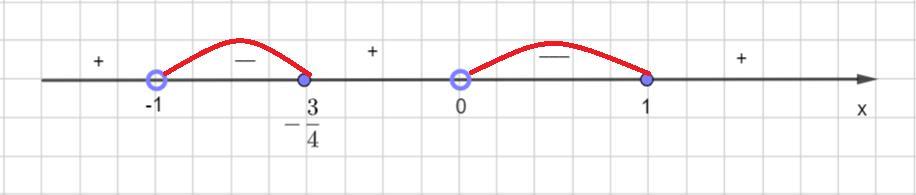
Решим данное неравенство методом интервалов. Отметим на числовой прямой точки и определим знак на каждом интервале

( числовая врямая во вложении).

Тогда получим

$-1 < t\leq -\dfrac{3}{4}$                  или          $0 < t\leq 1$

Вернемся к замене и получим

1)

$-1 < \log{_2}(x-1)\leq -\dfrac{3}{4} ;\\\\\dfrac{1}{2} < x-1\leq 2^{-\dfrac{3}{4} } ;\\\\\dfrac{1}{2} < x-1\leq \dfrac{1}{2^{\frac{3}{4} } } ;\\\\\dfrac{1}{2} < x-1\leq \dfrac{1}{\sqrt[4]{8} } ;\\\\\dfrac{1}{2} +1 < x\leq \dfrac{1}{\sqrt[4]{8} } +1;\\\\\dfrac{3}{2} < x\leq \dfrac{1}{\sqrt[4]{8} } +1$

2)

$0 < \log{_2}(x-1)\leq1 ;\\\\1 < x-1\leq 2;\\\\1+1 < x\leq 2+1;\\\\2 < x\leq 3$

Проверим ОДЗ и получим, что   решением неравенства является

х∈ $\left(\dfrac{3}{2};\dfrac{1}{\sqrt[4]{8} } +1\right]$ ∪ $(2;3]$