Предмет: Геометрия,
автор: denkuty06
Основанием пирамиды является треугольник со сторонами 13см, 14см, 15см. Вершина пирамиды удалена от каждой стороны основания на расстоянии 5см. Найдите объем пирамиды.
zmeura1204:
Нужно найти площадь основания, и радиус вписанной окружности.
По теореме Пифагора найти высоту h=√(5²-r²). И дальше найти обьем.
Ответы
Автор ответа:
2
Ответ:
84см³
Решение:
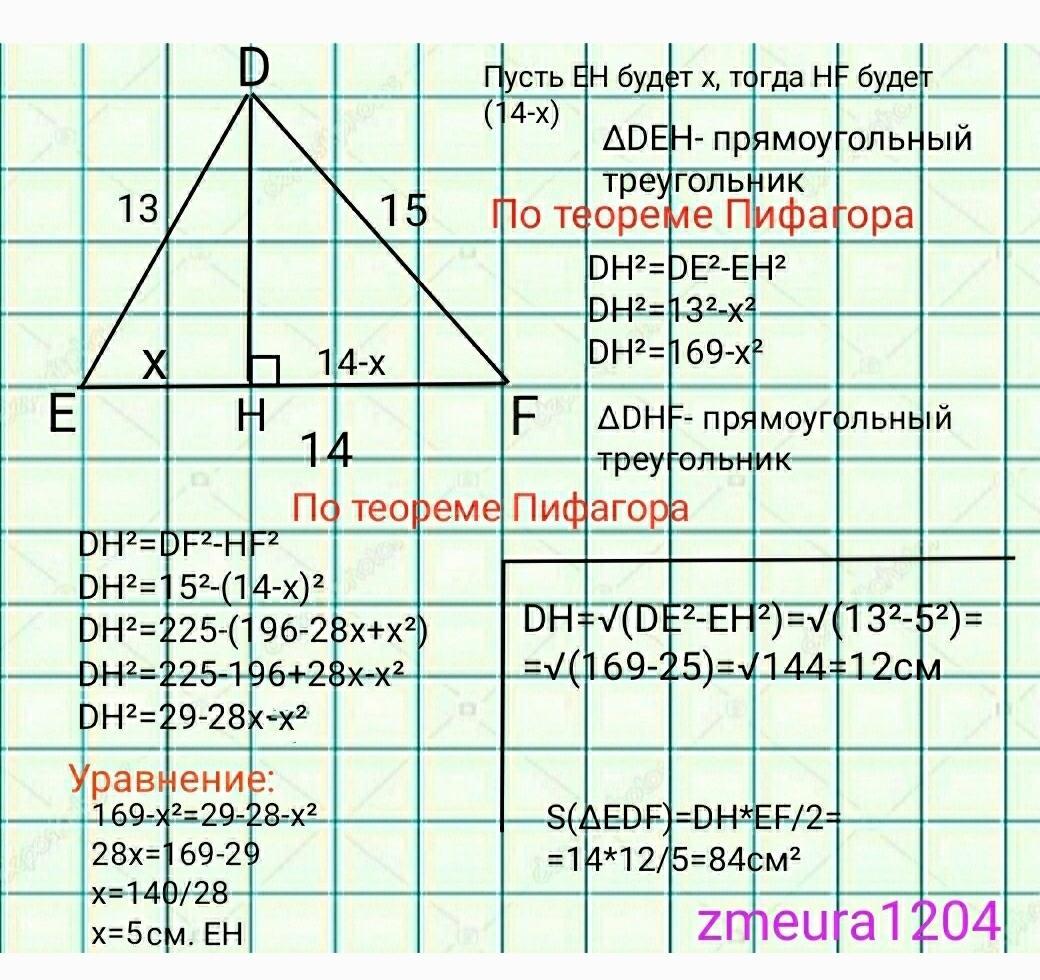
Треугольник со сторонами 13см;14см;15см. Высотой проведенной к стороне 14, делит треугольник на два прямоугольных треугольника со сторонами 13см;5см;12см и 15см;9см;12см, где 12 высота проведенная к стороне 14см.
S(∆DFE)=DH*EF/2=12*14/2=
=84см² площадь основания.
r=KO
r=S(∆DFE)/p, где р-полупериметр треугольника
р=(13+14+15)/2=42/2=21см.
KO=84/21=4cм.
∆SKO- прямоугольный треугольник.
По теореме Пифагора
SO=√(SK²-KO²)=√(5²-4²)=3см
V=⅓*S(∆DFE)*SO=84*3/3=84см³
84см³
Решение:
Треугольник со сторонами 13см;14см;15см. Высотой проведенной к стороне 14, делит треугольник на два прямоугольных треугольника со сторонами 13см;5см;12см и 15см;9см;12см, где 12 высота проведенная к стороне 14см.
S(∆DFE)=DH*EF/2=12*14/2=
=84см² площадь основания.
r=KO
r=S(∆DFE)/p, где р-полупериметр треугольника
р=(13+14+15)/2=42/2=21см.
KO=84/21=4cм.
∆SKO- прямоугольный треугольник.
По теореме Пифагора
SO=√(SK²-KO²)=√(5²-4²)=3см
V=⅓*S(∆DFE)*SO=84*3/3=84см³
Приложения:

Спасибо большое!
Похожие вопросы
Предмет: Русский язык,
автор: maripylka
Предмет: Английский язык,
автор: dawn10803
Предмет: Русский язык,
автор: KrupnovNikita2004
Предмет: Русский язык,
автор: chudakova2002
Предмет: Английский язык,
автор: Аноним