Question

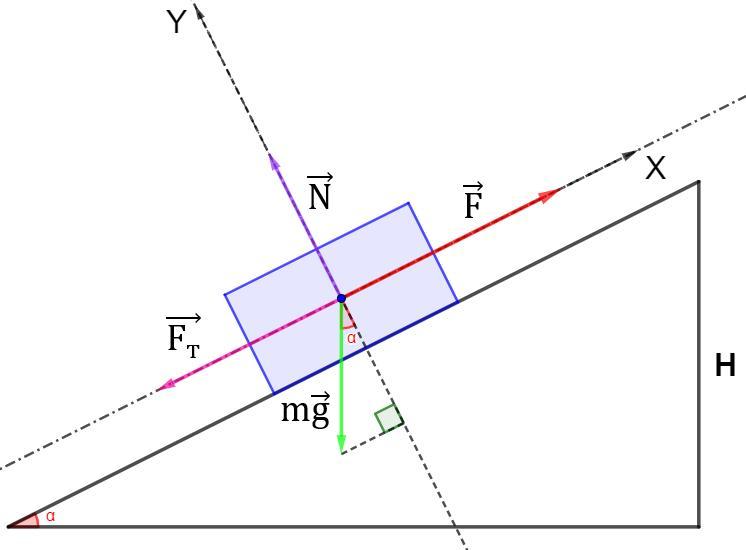
Тіло масою 200 г починають піднімати похилою площиною вгору із силою 4 Н, яка напрямлена вздовж похилої площини. Ця площина утворює кут 60° з горизонтом. Якої

швидкості набуде тіло, коли проїде 80 см? Коефіцієнт тертя тіла об похилу площину

дорівнює 0,4.

Answer 1

Ответ:

Тело приобретет скорость приблизительно 5,4 м/c

Объяснение:

Дано:

$m =$ 0,2 кг

$F =$ 4 H

$\alpha =$ 60°

$\mu =$ 0,4

$S =$ 0,8 м

$v_{0} =$ 0 м/c

$g =$ 10 м/c²

Найти:

$v_{k} \ - \ ?$

-------------------------------

Решение:

$\overrightarrow{F} + \overrightarrow{F_{T}} + \overrightarrow{N} + m\vec{g} = m\vec{a}$ - по второму закону Ньютона

$OX: F - F_{T} = ma \Longrightarrow \boxed{ a = \dfrac{F - F_{T}}{m} }$

$OY: N -mg \cos\alpha = 0; N = mg \cos\alpha$ - сила реакции опоры

$F_{T} = \mu N = \mu mg\cos \alpha$ - сила трения

$a = \dfrac{F - F_{T}}{m} = \dfrac{F - \mu mg\cos \alpha}{m}$

$\boxed{\boldsymbol{a = \dfrac{F - \mu mg\cos \alpha}{m} } }$ - ускорение

$v_{k}^{2} - v_{0}^{2} = 2aS;$ (по условию $v_{0} =$ 0 м/c, поэтому эту величину в дальнейшем можно не учитывать)

$v_{k}^{2} = 2aS \Longrightarrow v_{k} = \sqrt{2aS} = \sqrt{\dfrac{2S(F - \mu mg\cos \alpha)}{m}}$

$\boxed{ \boldsymbol{ v_{k} = \sqrt{\dfrac{2S(F - \mu mg\cos \alpha)}{m}} }}$

$v_{k} =$ √((2 * 0,8 м(4 H - 0,4 * 0,2 кг * 10 м/c² * cos 60°)) / (0,2 кг)) $\approx 5,4$ м/c

Ответ: $v_{k} \approx$ 5,4 м/c.