Предмет: Математика,
автор: garrzzza
Помогите пожалуйста, срочно
Приложения:
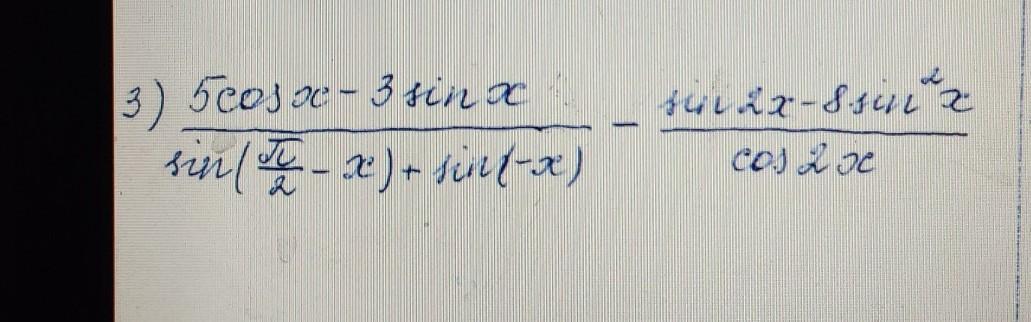
Ответы
Автор ответа:
1
Ответ:
3) Применяем формулу приведения , формулы синуса и косинуса двойных углов
,
, нечётность синуса
, тригонометрическую единицу
, формулу разности квадратов
.
Похожие вопросы
Предмет: Английский язык,
автор: роботехника
Предмет: Русский язык,
автор: nigorochka89gmailru
Предмет: Русский язык,
автор: Anny166
Предмет: Математика,
автор: irinabelova200
Предмет: Математика,
автор: lizok200740