Предмет: Геометрия,
автор: Аноним
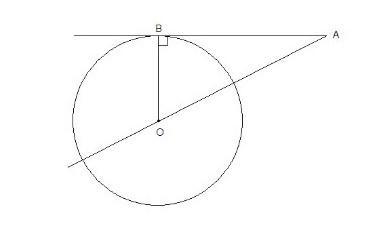
К окружности с центром в точке О проведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 20 , AO = 29 .
Ответы
Автор ответа:
0
Ответ:
21
Объяснение:
Проведем радиус ОВ.
Радиус, проведенный в точку касания, перпендикулярен касательной, значит
∠ОВА = 90°.
Из треугольника ОВА по теореме Пифагора:
ОВ = √(АО² - АВ²) = √(29² - 20²) = √((29 - 20)(29 + 20)) = √(9 · 49) = 3 · 7 = 21
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: кити311
Предмет: Русский язык,
автор: настя5349
Предмет: Українська мова,
автор: Mimgasik
Предмет: Английский язык,
автор: max100q
Предмет: Физика,
автор: atrembatman2017