Предмет: Геометрия,
автор: chertOFFka777
диагональ прямоугольной трапеции делит острый угол пополам, а вторую диагональ в отношении 8:6. Найдите площадь трапеции, если ее высота равна 12см.
Ответы
Автор ответа:
0
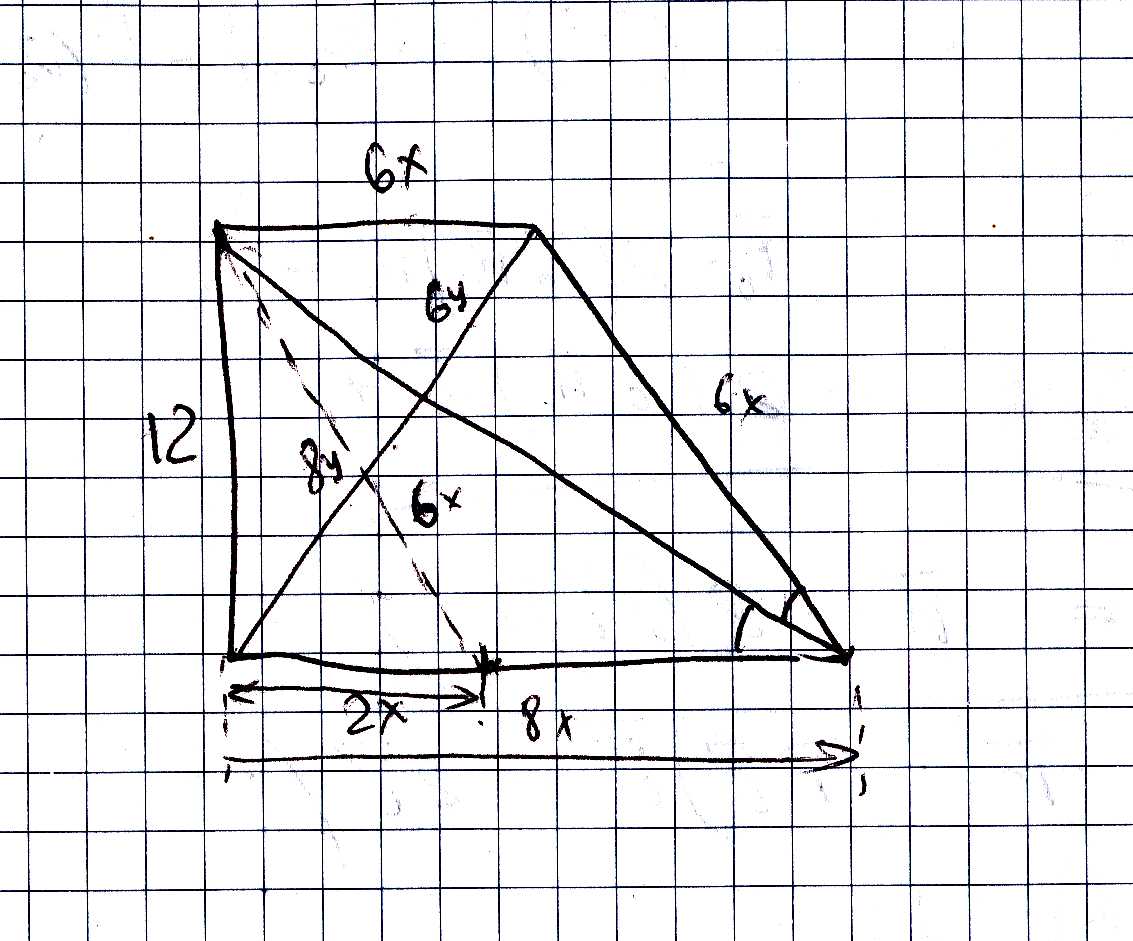
Трапеция нарисована на чертеже. Большое основание относится к боковой стороне, как 8:6 - свойство биссектрисы. Далее, треугольники, образованные основаниями и кусками диагоналей, с общей вершиной в точке их (диагоналей) пересечения, подобны. Поэтому большое основание относится к малому ТОЖЕ как 8:6.
Пусть х - некая мера длинны, так что большое основание 8*х, малое 6*х, боковая сторона 6*х. Тогда
12^2 + (8*x - 6*x)^2 = (6*x)^2; (построили треугольник, проведя прямую, параллельную боковой стороне через другую вершину)
Отсюда х = (3/2)*корень(2); средняя линяя равна 7*х = (21/2)*корень(2),
а площадь = 12*(21/2)*корень(2) = 126*корень(2)
Приложения:
Похожие вопросы
Предмет: Математика,
автор: dianaanickina107
Предмет: Другие предметы,
автор: vucoojji
Предмет: Биология,
автор: diman2007a5
Предмет: Физика,
автор: being