площадь осевого сечения усеченного конуса равна 81 см кв. Найдите радиус большего основания усеченного конуса, если радиус меньшего основания равен 2,5 см, а длина образующей 9 см.
Ответы
Ответ:
Ответа нет.
Объяснение:
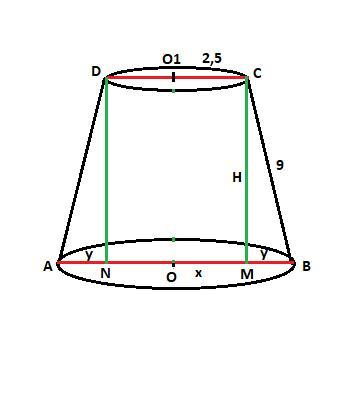
Смотрите рисунок.
Верхнее основание:
CO1 = O1D = 2,5 см, CD = 2*2,5 = 5 см.
Образующая: BC = AD = 9 см.
Осевое сечение усеченного конуса - равнобочная трапеция ABCD.
Площадь этого сечения, то есть трапеции: S = 81 см^2.
Найти радиус нижнего основания OA = OB.
Решение:
Обозначим нижнее основание конуса AB = x.
Опускаем высоты DN = CM = H на нижнее основание. Оно разбивается на отрезки:
AB = AN + NM + MB
При этом AN = MB = y, NM = CD = 5 см
x = 5 + 2y
Для треугольника CMB по теореме Пифагора:
y^2 + H^2 = 9^2
H = √(81 - y^2)
Площадь трапеции:
S = (AB + CD)*CM/2 = (5 + 2y + 5)*H/2 = (y + 5)*√(81 - y^2) = 81
(y + 5)*√(81 - y^2) = 81
Возводим всё уравнение в квадрат:
(y^2 + 10y + 25)(81 - y^2) = 81^2
81y^2 + 810y + 2025 - y^4 - 10y^3 - 25y^2 = 6561
0 = 6561 - 81y^2 - 810y - 2025 + y^4 + 10y^3 + 25y^2
y^4 + 10y^3 - 56y^2 - 810y + 4536 = 0
Уравнение явно не школьное, и как его решать, неизвестно.
Я проверил это уравнение в Вольфрам Альфе - оно не имеет действительных решений.
Видимо, в задаче опечатка, или она вообще неправильная.