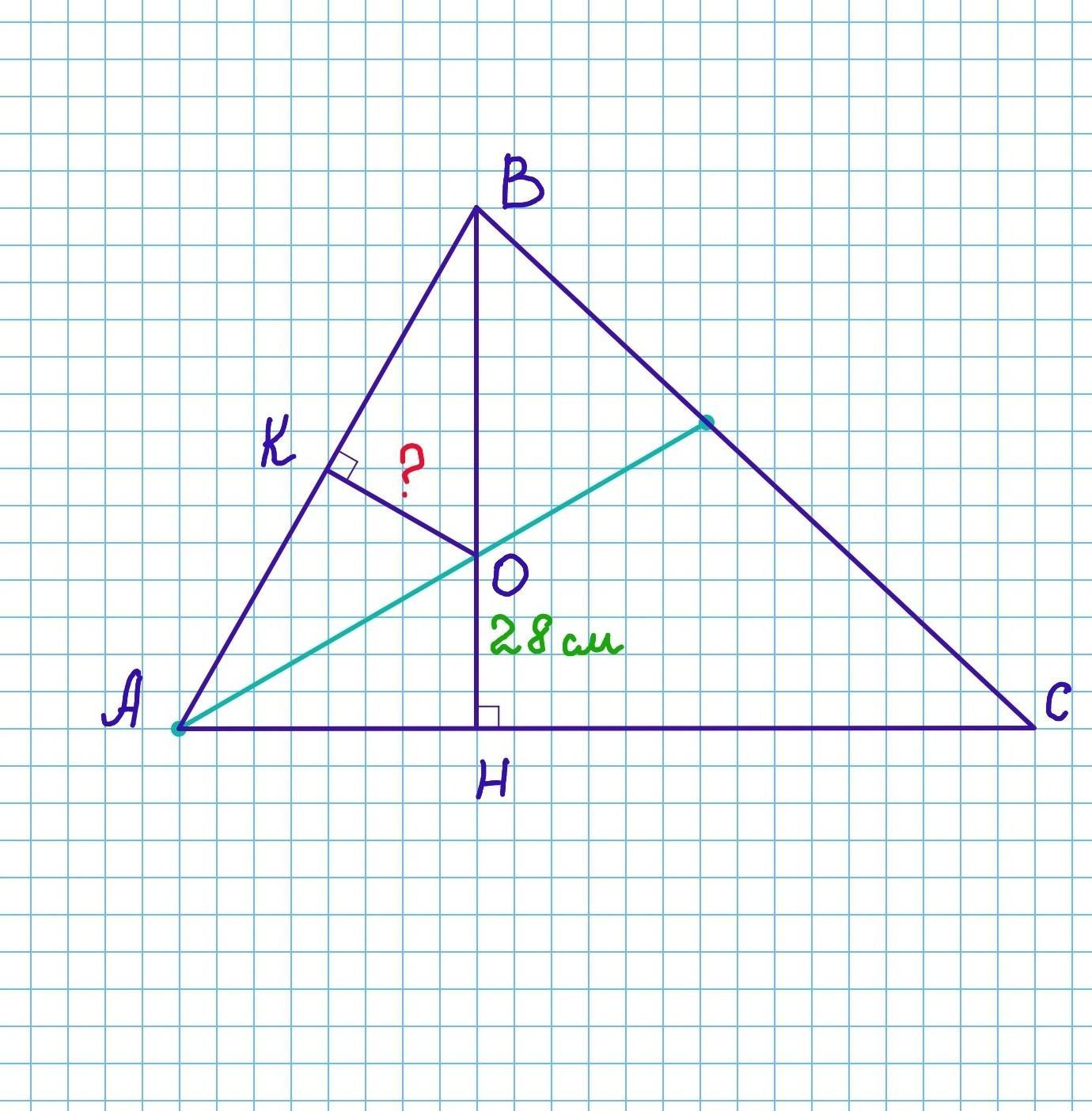
!! Помогите пожалуйста!! В остроугольном ΔABC биссектриса ∠ A пересекает высоту BH в точке O , причём OH = 28 см. Найти расстояние от точки O до прямой AB
Ответы
Ответ:
Расстояние от точки O до прямой AB равно 28 см
Объяснение:
В остроугольном ΔABC проведём высоту ВН. Биссектриса ∠A пересекает высоту BH в точке O , ОН=28 см.
Из точки О проведём перпендикуляр ОК к стороне АВ. Это и будет расстоянием от точки O до прямой AB.
Найдём ОК.
Рассмотрим прямоугольные треугольники АОН(∠Н=90°) и АОК(∠К=90°).
Так как АО - биссектриса, то ∠ОАК=∠ОАН, АО - общая.
Треугольники равны по гипотенузе и острому углу.
Из равенства треугольников следует равенство соответствующих катетов:
ОК=ОН=28 см
Также по определению биссектрисы угла:
Биссектриса - это геометрическое место точек, равноудалённых от сторон угла.
То есть если из любой точки, лежащей на биссекстрисе, провести перпендикуляры к сторонам угла, они будут равны.
Поэтому, так как точка О - лежит на биссектрисе ∠ВAС, ОН⟂АС и ОК⟂АВ, АС и АВ - стороны угла, то ОН=ОК.