Question

ДАЮ 40 Баллов
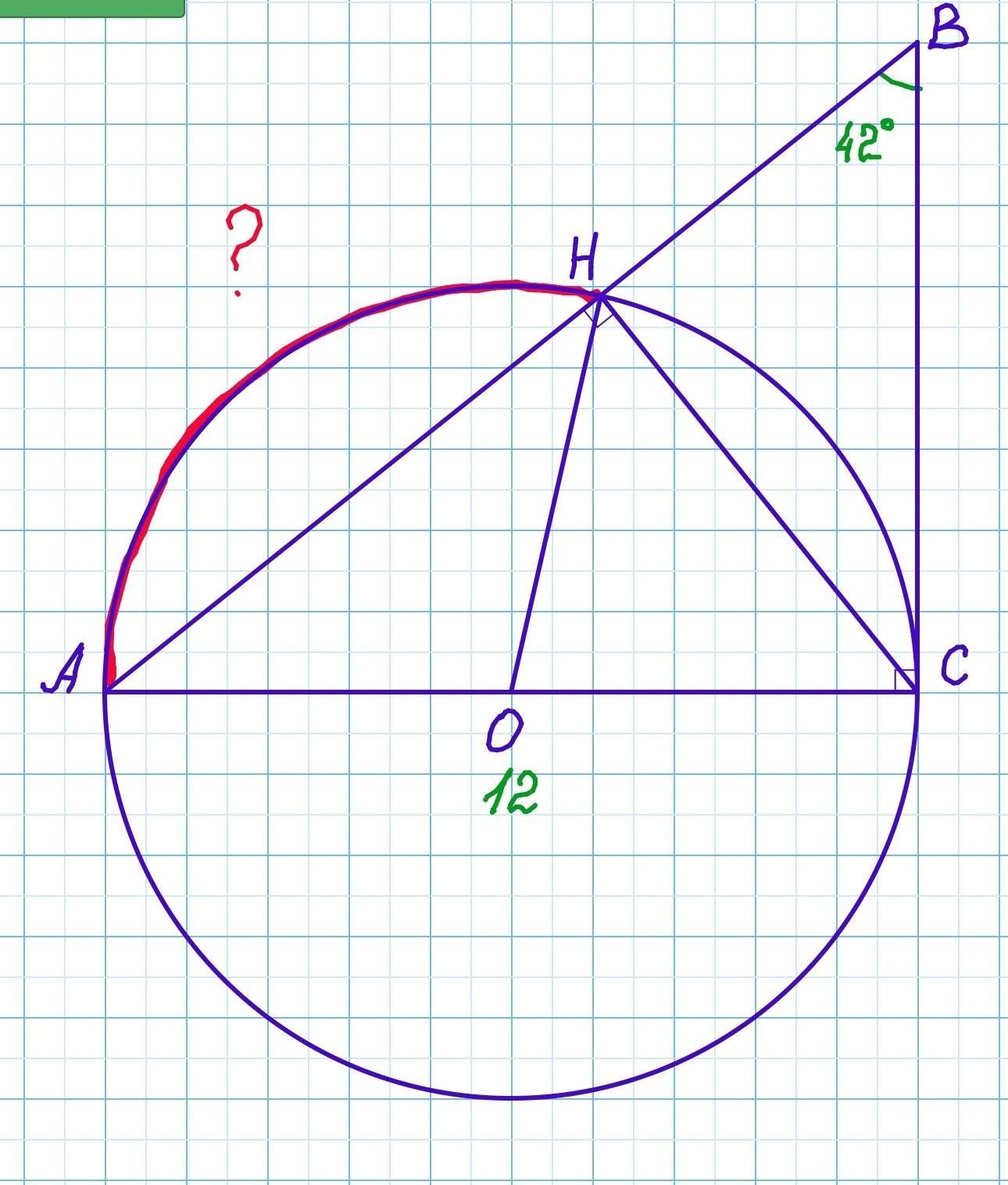
Задан прямоугольный треугольник ABC, в котором угол C – прямой, угол B = 42° и AC = 12. На катете AC как на диаметре построена окружность. Найдите длину дуги этой окружности, которая находится вне треугольника и отсекается гипотенузой AB.

Answer 1

Ответ:

Длина дуги окружности, которая находится вне треугольника АВС и отсекается гипотенузой AB равна 2,8π

Объяснение:

Задан прямоугольный треугольник ABC(∠C=90°), ∠B = 42° и AC = 12.

На катете AC как на диаметре построена окружность с центром в точке О.

Найти: длину дуги АН.

• Для нахождения длины дуги окружности необходимо использовать формулу:

$l = \frac{\pi R}{180^\circ} \times \alpha$

где R - радиус окружности, α - центральный угол, который опирается на эту дугу.

Радиус окружности равен половине диаметра: R=½•AC=½•12=6 ед.

Центральный угол - это угол, образованный двумя радиусами, вершина которого лежит в центре окружности.

На дугу АН опирается центральный угол АОН.

Найдём ∠АОН.

∠АСН - вписанный угол, опирающийся на дугу АН.

• Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.

Следовательно ∠АОН=2×∠АСН.

Рассмотрим прямоугольный треугольник АВС (∠С=90°)

Сумма острых углов прямоугольного треугольника равна 90°.

∠ВАС=90°-∠B=90°-42°=48°.

Точка Н лежит на окружности с диаметром АС, поэтому ∠АНС=90°. △АНС - прямоугольный.

∠АСН=90°-∠НАС=90°-48°=42°.

∠АОН=2×42°=84°.

Тогда длина дуги АН:

$l = \frac{\pi \times 6}{180^\circ} \times 84^\circ = 2, 8\pi$