Question

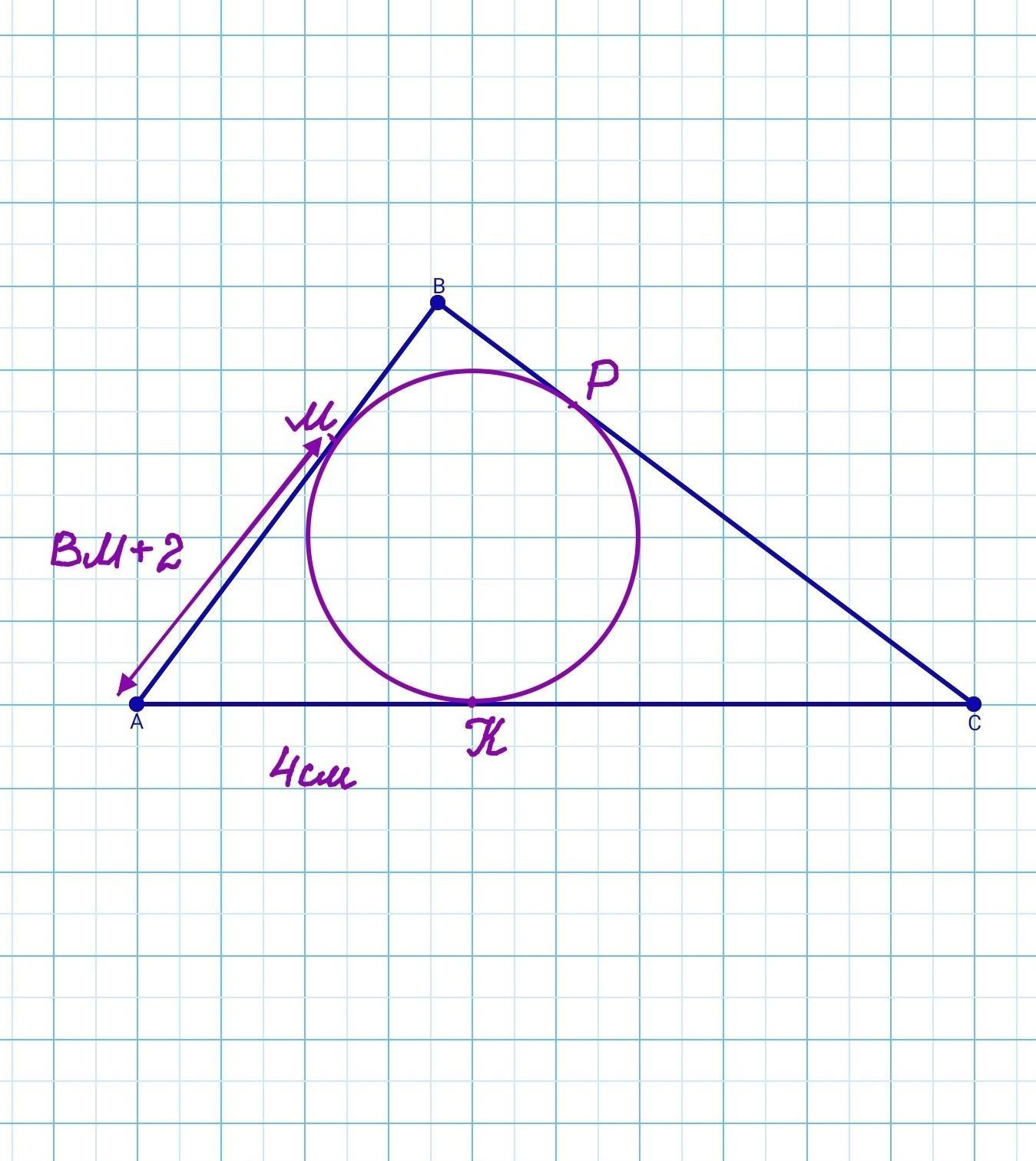
Периметр трикутника ABC, описаного навколо кола, дорiвнює 24см. Коло дотикається сторони AB у точці М, причому вiдрiзок АМ на 2см БIЛЬШИЙ 33 вiдрiзок ВМ. Знайдіть сторони трикутника, якщо точка дотику зі стороною АС вiддалена вiд вершини А на 4см.​

Answer 1

Ответ:

АВ=6 см, ВС = 8см, АС=10 см

Объяснение:

Периметр треугольника АВС равен 24см. В треугольник вписана окружность. М - точка касания окружности и стороны АВ. АМ>ВМ на 2см. АК=4см.

Найдём АВ, ВС, АС.

• Отрезки касательных к окружности, проведенных из одной точки, равны.

АМ=АК=4см,

Так как АМ больше ВМ на 2см, то ВМ=АМ-2=4-2=2см.

Сторона АВ=АМ+ВМ=4+2=6 см

ВР=ВМ=2см.

Пусть СР=СК= х см.

Тогда периметр треугольника АВС будет равен:

АВ+ВС+АС=24

АВ+ВР+СР+СК+АК=24

6+2+х+х+4=24

2х=12

х=6

СР=СК= 6 см.

Итак, сторона ВС=ВР+СР=2+6=8 см

сторона АС=АК+СК=4+6=10 см.

АВ=6 см