Предмет: Алгебра,
автор: polinagalina06
2.Найдите значение выражения
Приложения:
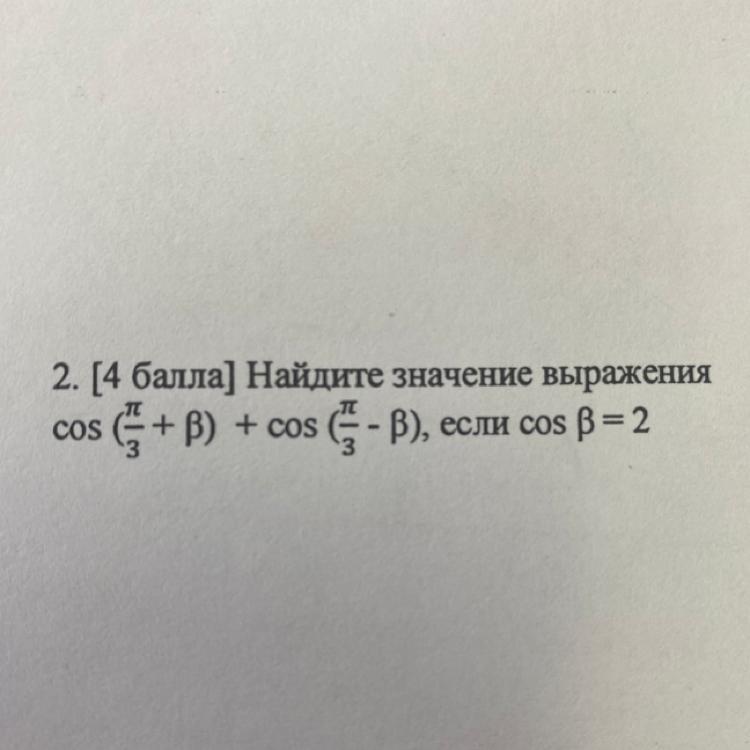
Ответы
Автор ответа:
0
Ответ:
Пользуемся формулой суммы косинусов:
.
Подставить мы не можем, так как значения функции y=cosx не могут превосходить 1 ,
.
Условие задано некорректно .
Похожие вопросы
Предмет: Английский язык,
автор: ттттттиитл
Предмет: Русский язык,
автор: Marinedno2016
Предмет: Русский язык,
автор: виктория992
Предмет: Английский язык,
автор: ali060357