Предмет: Математика,
автор: sagana211187
Помогите пожалуйста решить!!!!
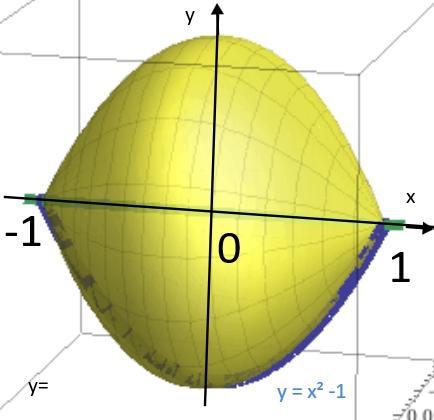
Вычислить объем тела вращения вокруг оси ох y=x^2-1 y=0
Ответы
Автор ответа:
1
Ответ:
объем тела вращения
Пошаговое объяснение:
у = х² -1
Формула для расчета тела вращения вокруг оси ОХ
Прежде всего рисуем график функций у = х² -1 и у=0.
Их точки пересечения и есть границы интегрирования
b= (-1)
a = 1
Теперь считаем определенный интеграл
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: conik8989
Предмет: Русский язык,
автор: ааппаапп
Предмет: Русский язык,
автор: янина678
Предмет: Литература,
автор: halal9