Предмет: Математика,
автор: dimamazar200
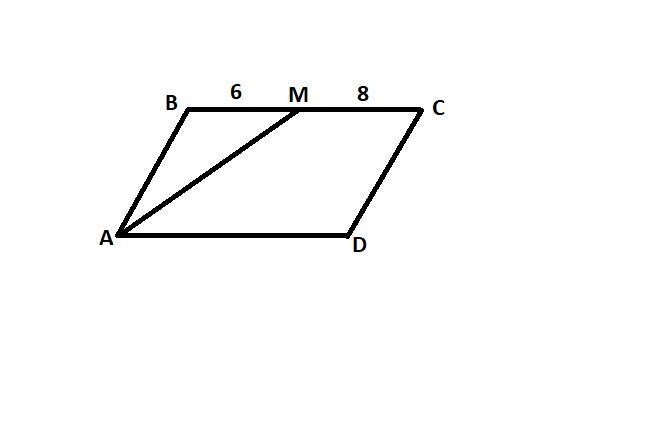
Биссектриса острого угла параллелограмма делит его сторону на отрезки 6 см и 8 см, считая от вершины тупого угла параллелограмма. Найдите периметр параллелограмма.
Ответы
Автор ответа:
1
Ответ:
Периметр параллелограмма равен 40 см.
Пошаговое объяснение:
Дано:
ABCD - параллелограмм, АМ - биссектриса ∠BAD, ВM = 6, МС = 8.
Найти:
Решение:
∠BAM = ∠DAM (т.к. по условию АМ - биссектриса ∠BAD),
∠BMA = ∠DAM (как внутренние накрест лежащие углы при AD ║ BC и секущей AM), отсюда мы можем сделать вывод, что ∠BAM = ∠AMB.
Тогда получается, что ΔABM - равнобедренный.
Тогда ВА = ВМ = 6см, а ВС = 8 + 6 = 14см.
см.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: KraRom
Предмет: Окружающий мир,
автор: energe1
Предмет: Английский язык,
автор: света2110
Предмет: Окружающий мир,
автор: Аноним
Предмет: Химия,
автор: liver1892d