Question

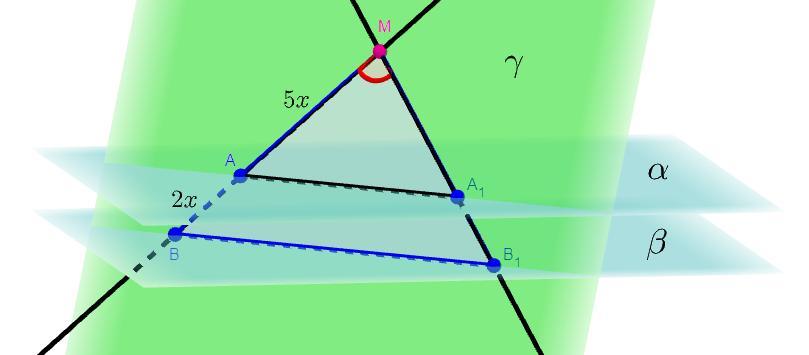
из точки М , находящейся вне двух параллельных плоскостей,проведены две прямые,пересекающие плоскости соответственно в точках А, В и А1,В1.найдите длину отрезка АА1, если ВВ1=28 см,а МА: АВ=5:2.​

Answer 1

Ответ:

$\LARGE \text{\boxed{ \boxed{\boldsymbol{ AA_{1} = 20}} } }$ см

Длинна отрезка $AA_{1}$ равна 20 см

Объяснение:

Дано: $BB_{1} =$ 28 см; $A, A_{1} \in \alpha;B, B_{1} \in \beta; \alpha \parallel \beta$, MA : AB = 5 : 2,

точки M,A,B - лежат на одной прямой, точки $M,A_{1},B_{1}$ - лежат на одной прямой

Найти: $AA_{1} \ - \ ?$

Решение:

По следствию из аксиом стереометрии через две пересекающиеся прямые можно провести плоскость, и притом только одну, тогда так как по условию, тогда так как по условию $M \in AB, A_{1}B_{1}$, то  $AB \cap A_{1}B_{1} =M$ и через прямые $AB$ и $A_{1}B_{1}$ проведем плоскость $\boldsymbol \gamma$ (именно данную плоскость однозначно задают прямые $AB$ и $A_{1}B_{1}$).

Так как по построению $AB \subset \gamma$, то $\boldsymbol{ A,B \in \gamma }$.

Так как по построению $A_{1}B_{1} \subset \gamma$, то $\boldsymbol{ A_{1},B_{1} \in \gamma }$.

По аксиоме прямой и плоскости (прямая, проходящая через две точки плоскости, лежит в этой плоскости), так как $\boldsymbol{ A,B,A_{1},B_{1} \in \gamma }$,

то $\boldsymbol{ AA_{1} \subset \gamma}$ и $\boldsymbol{BB_{1} \subset \gamma}$.

По аксиоме пересечения плоскостей (если две плоскости имеют общую точку, то их пересечение есть прямая (из чего следует, что плоскости пересекаются по прямой), тогда так как по условию

$AA_{1} \subset \alpha$ и $AA_{1} \subset \gamma$, то $\boldsymbol{ \gamma \cap \alpha = AA_{1}}$; $BB_{1} \subset \beta$ и $BB_{1} \subset \gamma$, то $\boldsymbol{ \gamma \cap \beta = BB_{1}}$.

По теореме линии пересечения двух параллельных плоскостей третьей плоскостью параллельны, тогда так как по условию $\alpha \parallel \beta$ и

$\gamma \cap \alpha = AA_{1}, \gamma \cap \beta = BB_{1}$, то $\boldsymbol{ AA_{1} \parallel BB_{1}}$.

Введем коэффициент пропорциональности $x$, тогда согласно условию $\boldsymbol{MA = 5x}$, а $\boldsymbol{AB = 2x}$.

По основному свойству отрезка:

$\boldsymbol{MB =} MA + AB = 5x + 2x = \boldsymbol{ 7x}$.

Треугольник $\boldsymbol{ зMAA_{1} \sim зMBB_{1}}$ по двум углам, так как угол $\angle BMB_{1}$ - общий, а угол  $\angle MAA_{1} = \angle MBB_{1}$ по теореме как соответственные углы при параллельных прямых $AA_{1}, BB_{1} (AA_{1} \parallel BB_{1})$ и секущей MB.

Так как треугольник $зMAA_{1} \sim зMBB_{1}$, то по свойствам подобных треугольников:

$\displaystyle \frac{AA_{1}}{BB_{1}} = \frac{MA}{MB} \Longrightarrow \boxed{\boldsymbol{ AA_{1} = \frac{BB_{1} \cdot MA}{MB}}} = \frac{28 \cdot 5x}{7x} = \frac{28 \cdot 5}{7} = 4 \cdot 5 = \boldsymbol{20}$ см.