Предмет: Математика,
автор: keitjony
Помогите пожалуйста, сложение вычитание дробей с одинаковыми знаменателями нужно провести в общему
Приложения:
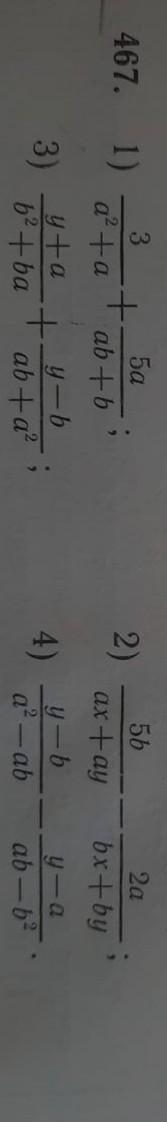
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Приложения:

Автор ответа:
1
1)
2)
3)
4)
Похожие вопросы
Предмет: Другие предметы,
автор: Dodiwko
Предмет: Английский язык,
автор: s2fag
Предмет: Українська мова,
автор: Сатаней45
Предмет: Литература,
автор: dashaaa82
Предмет: География,
автор: Аноним