Предмет: Геометрия,
автор: Аноним
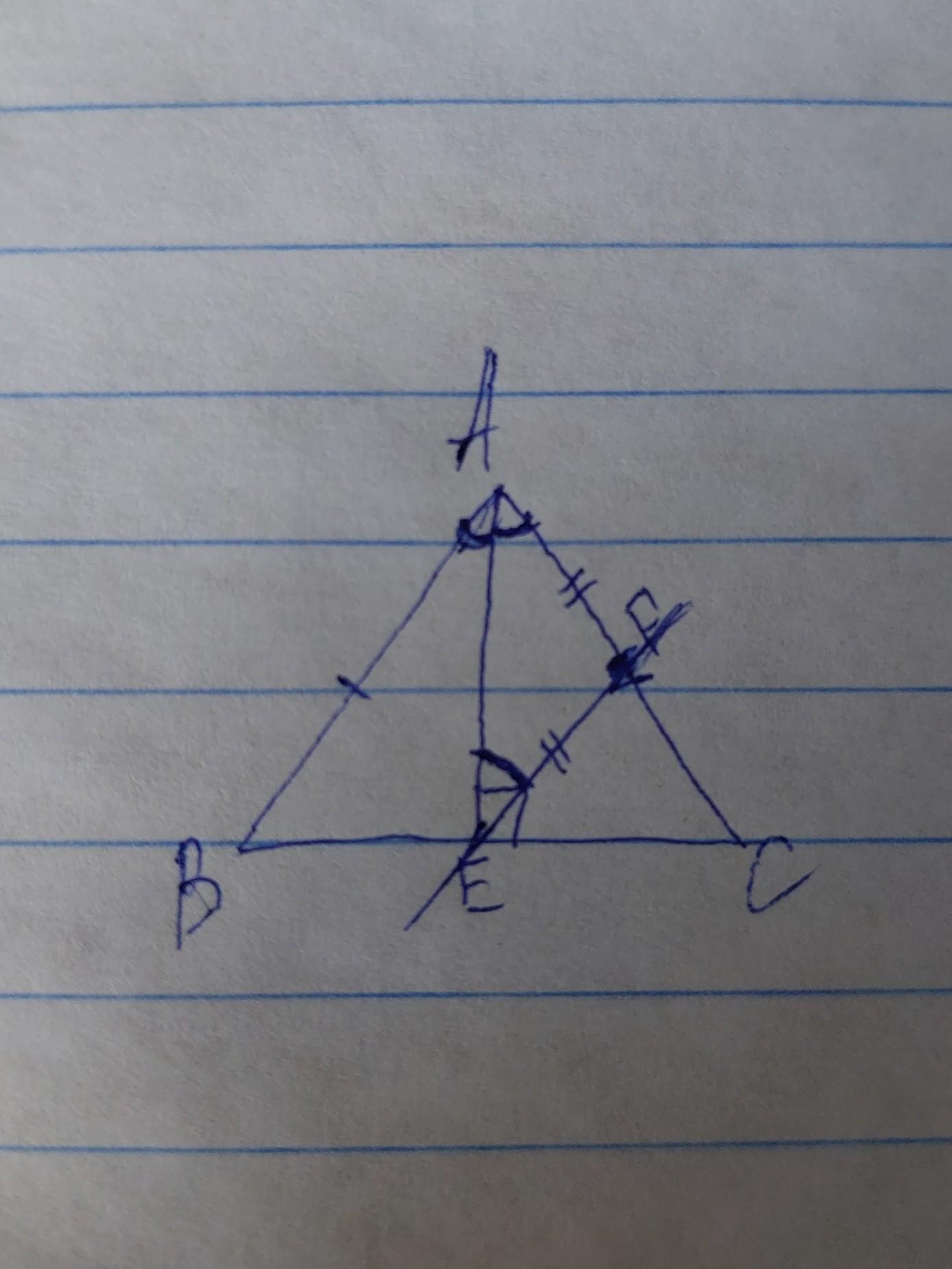
В треугольнике ABC известно, что AB=AC, отрезок AE - высота. На стороне AC отметили точку F такую, что FE=AF. Докажите, что EF||AB.
Ответы
Автор ответа:
17
Ответ:
ЕF||AB
Объяснение:
в ^АВС АВ=АС(боковые стороны), значит ^АВС равнобедренный.
слеледовательно и углы при основании ВС равны (угол В= углу С)
Высота АЕ это медиана и биссектриса (св-во р.б треугольника)
значит угол ВАЕ=ЕАС
По условию задачи ЕF=AF, значит треуг-ник АFE равнобедренный (т.к. это боковые стороны)
значит и углы АЕF и FAE равны, а угол FAE равен углу EAB.
Следовательно и угол FEA равен углу EAB, а это накрестлежащие углы при секущей АЕ и они равны.
Значит ЕF||AB.
Надеюсь все понятно, ориентируйся по рисунку, удачи!
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: ket24077
Предмет: Русский язык,
автор: neman1
Предмет: Окружающий мир,
автор: Сарафанчика
Предмет: Английский язык,
автор: Troveprofi
Предмет: Русский язык,
автор: varvara4937