Предмет: Алгебра,
автор: Reideen
Задание приложено...
Приложения:
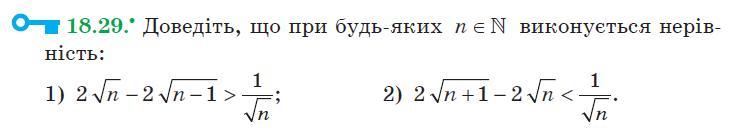
Ответы
Автор ответа:
1
Ответ:
Так как по условию , то при решении можно не учитывать ОДЗ
1)
- верно
2)
- верно
Похожие вопросы
Предмет: Українська мова,
автор: linaPovopoznik
Предмет: Технология,
автор: Аноним
Предмет: Технология,
автор: nikolaeffnikita
Предмет: Биология,
автор: nebesnyyangel
Предмет: Английский язык,
автор: kipr2303230323032303