Question

С полным решением и чертежом

Answer 1

Ответ:

180 см²

Объяснение:

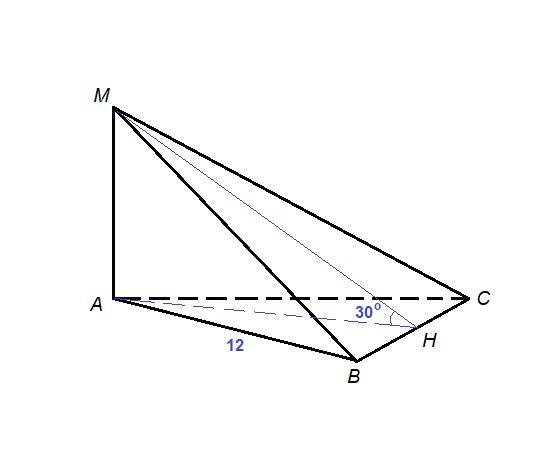
Построим линейный угол двугранного угла между плоскостями (МВС) и (АВС).

Пусть Н - середина ВС. Тогда АН - медиана и высота правильного треугольника АВС.

АН⊥ВС.

АН - проекция МН на плоскость (АВС), значит МН⊥ВС по теореме о трех перпендикулярах.

∠МНА = 30° - линейный угол двугланного угла между плоскостями (МВС) и (АВС).

По формуле высоты равностороннего треугольника:

$AH=\dfrac{AB\sqrt{3}}{2}=\dfrac{12\sqrt{3}}{2}=6\sqrt{3}$

AH = 6√3 см

ΔМАН:  ∠МАН = 90°,

 $tg\angle MHA =\dfrac{MA}{AH}$

 $\dfrac{\sqrt{3}}{3}=\dfrac{MA}{6\sqrt{3}}$

$MA=\dfrac{6\sqrt{3}\cdot \sqrt{3}}{3}=6$

MA = 6 см

МН = 2 · МА = 2 · 6 = 12 см (по свойству катета, лежащего против угла в 30°)

Площадь основания:

$S_{ABC}=\dfrac{AB^2\sqrt{3}}{4}=\dfrac{12^2\sqrt{3}}{4}=\dfrac{144\sqrt{3}}{4}=36$ см²

ΔМАВ = ΔМАС по двум катетам:

• ∠МАВ = ∠МАС = 90°,
• МА - общаий катет,
• АВ = АС (ΔАВС равносторонний).

$S_{MAB}=S_{MAC}=\dfrac{1}{2}MA\cdot AB=\dfrac{1}{2}\cdot 6\cdot 12=36$ см²

Площадь третьей боковой грани:

$S_{MBC}=\dfrac{1}{2}BC\cdot MH=\dfrac{1}{2}\cdot 12\cdot 12=72$ см²

Площадь поверхности пирамиды:

$S=S_{ABC}+2\cdot S_{MAB}+S_{SBC}$

S = 36 + 2 · 36 + 72 = 36 + 72 + 72 = 180 см²